Statistical Principles?
Larry Wasserman
There are some so-called principles of statistical inference that have names like, the Sufficiency Principle (SP), the Conditionality Principle (CP) and the Likelihood Principle (LP).
Birnbaum (1962) proved that CP and SP imply LP. (But see Mayo 2010). Later, Evans Fraser and Monette (1986) proved that CP alone implies LP (so SP is not even needed).
All of this generates controversy because CP (and SP) seem sensible. But LP is not acceptable to most statisticians. Indeed, all of frequentist inference violates LP, so if we adhered to LP we would have to abandon frequentist inference. In fact, as I’ll explain below, LP pretty much rules out Bayesian inference contrary to the claims of Bayesians.
How can CP be acceptable and LP not be acceptable when CP logically implies LP?
The reason is that the principles are bogus. What I mean is that, CP might seem compelling in a few toy examples. That doesn’t mean it should be elevated to the status of a principle.
1. The Principles
SP says that: if two experiments yield the same value for a sufficient statistic, then the two experiments should yield the same inferences.
CP says that: if I flip a coin to choose which of two experiments to conduct, then inferences should depend only on the observed experiment. The fact that I could have chosen the other experiment should not affect inferences. In more technical language, the coin flip is ancillary, (its distribution is completely known), and inferences should be conditional on the ancillary.
LP says that: two experiments that yield proportional likelihood functions should yield identical inferences.
Frequentist inference violates LP because things like confidence intervals and p-values depend on the sampling distributions of estimators and so on, which involves more than just the observed likelihood function.
Bayesians seem to embrace LP and indeed use it as an argument for Bayesian inference. But two Bayesians with the same likelihood can get different inferences because they might have different priors (and hence different posterior distributions). This violates LP. Whenever I say this to people, the usual reply is: but Birnbaum’s theorem only applies to one person at a time. But this is not true. There is no hidden label in Birnbaum’s theorem that says: Hey, this theorem only applies to one person at a time.
2. CP Is Bogus
Anyway it doesn’t matter. The main point is that CP (and hence LP) is bogus. Just because it seems compelling that we should condition on the coin flip in the simple mixture example above, it does not follow that conditioning is always good. Making a leap from a simple, toy example, to a general principle of inference is not justified.
Here is a simple example. I think I got it from Jamie Robins. You observe
where
and . To be concrete, let’s say that
but each
is a vector of length
and
is huge;
for example. We want to estimate
. This is just linear regression with a large number of covariates.
Suppose we have some extra information: we are told that the covariates are independent. The “best” estimator (the maximum likelihood estimator) is obtained by conditioning on all the data.
This means we should estimate the vector by least squares. But, the least squares estimator is useless when
. We could regularize by putting a penalty or a prior. But the resulting estimators will have terrible behavior compared to the following “anti-conditioning” estimator. Just throw away most of the data. In particular, throw away all the covariates except the first one. Now do linear regression using only
and the first covariate. The resulting estimator
is then tightly concentrated around
with high probability. (This is because of the independence.)
In this example, throwing away data is much better than conditioning on the data. We are heavily violating LP.
There are lots of other examples of great procedures that violate LP. Randomization is a good example. Methods based on randomization (such as permutation tests) are wonderful things but adherents to CP (and hence LP) are precluded from using them. The same applies to data-splitting techniques.
The bottom line is this: if we elevate lessons from toy examples into grand principles we will be led astray.
Postscript: Since I mentioned Jamie, I should alert you that in the near future, I’ll be cross-posting on this blog and Cosma’s blog about a debate between me and Jamie versus a Nobel prize winner. Stay tuned.
Evans, M.J., Fraser, D.A.S. and Monette, G. (1986). On principles and arguments to likelihood. Canadian Journal of Statistics, 14, 181-194.
Birnbaum, Allan (1962). “On the foundations of statistical inference”. J. Amer. Statist. Assoc., 57 269-326.
Mayo, D. (2010). An Error in the Argument from Conditionality and Sufficiency to the Likelihood Principle. In Error and Inference: Recent Exchanges on Experimental Reasoning, Reliability and the Objectivity and Rationality of Science (D Mayo and A. Spanos eds.), 305-14.
20 Comments
Great read as usual. Maybe there’s some subtlety I missed, but in your small example, isn’t the solution you propose simply obtained with a different prior? As you said, the first prior that comes to mind is penalizing the L2 norm (as in ridge regression) but you might just as well use a sparsity-inducing norm penalization, rendering the coefficients for all other covariates 0.
Yes. Good point. You can pick a prior that forces the Bayes estimator to be the “anti-conditional” estimator
but the prior is supposed to represent your prior opinions about the parameters.
If you pick the prior just to force the Bayes estimator to be the desired frequentist
estimator then are you really doing Bayesian inference?
—LW
But *which* Bayes estimator? Estimators are just ways to summarize the posterior – so there are many one could use. Some estimators may end up giving sparse estimates, even when the prior and/or posterior give little (or zero) posterior support to sparseness in the true underlying parameters.
Just like there’s no “hidden label” in Birnbaum (which is a great point!) there’s nothing in Bayes that says one has to use the posterior mean/median/mode.
[q]How can CP be acceptable and LP not be acceptable when CP logically implies LP?[\q]
This reminds me of this quote.
“The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn’s lemma?” — Jerry Bona
Great post. “Principles” too often become dogma. The example you gave reminded me of an “ancillarity paradox” in a paper of Larry Brown’s:
Brown, L. D. “An Ancillarity Paradox Which Appears in Multiple Linear Regression”
Ann. Statist. Volume 18, Number 2 (1990), 471-493.
http://projecteuclid.org/euclid.aos/1176347602
He gave an example where the admissibility of the least squares estimator of the intercept in the Normal linear model depends on whether or not you condition on X. It is admissible only if X is fixed (i.e. you condition on X).
Indeed. As I recall. we were discussing that very paper by Larry Brown
when Jamie said: here is a another version of the same idea.
A central mistake is in thinking the LP follows even from restricting CP to the cases where it is plausible (irrelevant coin flip mixtures). I have argued this in the paper you cite and elsewhere but many are so used to the “proof” that they assume I must be wrong. I am writing a longer treatment this week as it happens. It remains to be seen whether the statistical community will accept the flaw in Birnbaum’s “breakthrough”!
“Bayesians seem to embrace LP and indeed use it as an argument for Bayesian inference. But two Bayesians with the same likelihood can get different inferences because they might have different priors (and hence different posterior distributions). This violates LP. Whenever I say this to people, the usual reply is: but Birnbaum’s theorem only applies to one person at a time.”
Huh. If you said it to me, I’d have replied that the LP states that inferences must depend *on the data under consideration* only through its likelihood function. It doesn’t prohibit inferences from depending on things other than data under immediate consideration, such as the available prior information. And I say this as one who was convinced by Mayo 2010 to examine Birnbaum’s argument more closely and concluded that it was flawed and that there is no compelling non-Bayesian reason to obey the LP. (It’s not clear to me if the error I think undermines Birnbaum’s argument is the same as the one Mayo identified.)
I think there’s a missing assumption in your description of the example of regression with d >> n, to wit, that each Xij has finite variance. Also, I think that saying that the estimator of beta_1 is “tightly concentrated” around the true value is overstating the case, since the estimator dumps the variance of the d-1 ignored covariates (scaled by the d-1 unknown parameters) directly into the estimate. I’d say rather that the resulting estimator’s variance is known to high accuracy, permitting reliable inference of the expected squared error.
“In this example, throwing away data is much better than conditioning on the data.”
This statement is not unconditionally true! It depends on the substantive prior knowledge one brings to the estimation problem.
I was avoiding technical details but yes we need some conditions on X.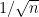 rate.
rate.
Then beta.hat1 concentrates at a
The ignored covariates have no effect at all.
–LW
I agree, the ignored covariates have no effect at all on the convergence rate. On the other hand, in terms of the variance of the estimator for the actual, finite data set notionally in front of us…
For future reference, when you write “tightly concentrated”, should that always be read as a statement about convergence rates?
Yes. Sorry for the lack of detail.

I mean:
—LW
Thanks for the fun post.
I don’t believe that this is a valid criticism of CP. It’s merely an indictment of ML. There are many examples where ML fails. Even the most the most ardent supporters of the LP stipulate that ML fails, yet would continue to contend that LP is applicable. My guess is that in your example they would say that LP still applies, but we don’t know how to work with large dimensional likelihoods.
I have a funny story where I was in a conversation with D R Cox. I asked him what he thought about CP and SP implying LP and he said “Oh that’s not true.” At which point someone asked “It has a mathematically correct proof. What’s not true?” To which he replied “The conclusion.”.
Fair enough. But there are examples where
(i) the likelihood function contains no information
(ii) yet there exist good estimators.
In fact, I am preparing a post on this right now.
—LW
Look forward to such examples, but I agree with Brian, I don’t see a problem here with likelihood as being the minimal sufficient statistic but rather how to work with it. It might make it clearer to write down a likelihood for each of the one hundred observations (the full likelihood bieng the multiple of these). Each one is a well defined function of the 100,001 unknown paramaters and if you had 100,001+ of these – what to do would be fairly straight forward.
This brings me to comment why I believe sufficiency itself is bogus.
Fisher’s original motivation was to summarize say two studies so that with just the summaries, a combined analysis could be done that was as good as having the raw data from both studies. Likelihood does that for _estimation_ but not for testing the fit of the model. The fit of model checked by the joint raw data might easily lead one to reject the model and the likelihoods under the rejected model will not necessarily be sufficient for the new model.
And today we can just archive the data for later re-use and hence summaries serve no purpose. (David Cox corrected me on that once saying they are useful for spliting up information for instance into that for estimation and that for testing fit.)
It seems to me that CP and SP are more plausible when formulated as claims about the evidential meaning of experimental outcomes (which is how Birnbaum formulated them) than when they are formulated as claims about what our inferences ought to depend on. The problem with this formulation from a likelihoodist or Bayesian point of view is that it seems to make LP toothless: a frequentist could accept Birnbaum’s proof without abandoning frequentist methods (as Birnbaum himself did) by denying that a statistical method must respect evidential equivalence.
Thanks for this. Clears a lot of stuff up that I was fuzzy on,
Dear Larry,
The way I see it, Birnbaum’s results are about equivalences of realizations of experiments; when expressed with the right set theoretical tools (equivalence relations over a well defined space of realizations), it seems to me that the tiny letters saying “Hey, this theorem only applies to one person (one prior) at a time.” are really there. Please, take a look at our short revision paper
http://proceedings.aip.org/resource/2/apcpcs/1073/1/96_1
especially Example 3. With two different priors, how would you come with a (necessarily reflexive) equivalence relation over the space of realizations?
Best regards,
Paulo.
P.S. I enjoy reading the blog. Please, keep posting.
Thanks
I was not able to get the paper.
LW
Here: http://www.ime.usp.br/~pmarques/papers/redux.pdf
Thanks
One Trackback
[…] on. Let me review a simplified version of Larry Brown’s (1990) example that I discussed here. You observe […]