LOST CAUSES IN STATISTICS I: Finite Additivity

LOST CAUSES IN STATISTICS I: Finite Additivity

I decided that I’ll write an occasional post about lost causes in statistics. (The title is motivated by Streater (2007).) Today’s post is about finitely additive probability (FAP).

Recall how we usually define probability. We start with a sample space and a -algebra of events . A real-valued function on is a probability measure if it satisfies three axioms:

(A1) for each .

(A2) .

(A3) If is a sequence of disjoint events then

The third axiom, countable additivity, is rejected by some extremists. In particular, Bruno de Finetti was a vocal opponent of (A3). He insisted that probability should only be required to satisfy the additivity rule for finite unions. If is only required to satisfy the additivity rule for finite unions, we say it is a finitely additive probability measure.

Axioms cannot be right or wrong; they are working assumptions. But some assumptions are more useful than others. Countable additivity is undoubtedly useful. The entire edifice of modern probability theory is built on countable additivity. Denying (A3) is like saying we should only use rational numbers rather than real numbers.

Proponents of FAP argue that it can express concepts that cannot be expressed with countably additive probability. Consider the natural numbers

There is no countably additive probability measure that puts equal probability on every element of . That is, there is no uniform probability on . But there are finitely additive probabilities that are uniform on . For example, you can construct a finitely additive probability for which for each . This does not contradict the fact that unless you invoke (A3).

You can also decide to assign probability 1/2 to the even numbers and 1/2 to the odd numbers. Again this does not conflict with each integer having probability 0 as long as you do not insist on countable additivity.

These features are considered to be good things by fans of FAP. To me, these properties make it clear why finitely additive probability is a lost cause. You have to give up the ability to compute probabilities. With countably additive probability, we can assign mass to each element and then we can derive the probability of any event by addition:

This simple fact is what makes probability so useful. But for FAP, you cannot do this. You have to assign probabilities rather than calculate them.

In FAP, you also give up basic calculation devices such as the law of total probability: if is a disjoint partition then

This formula is, in general, not true for FAP. Indeed, as my colleagues Mark Schervish, Teddy Seidenfeld and Jay Kadane showed, (see Schervish et al (1984)), every probability measure that is finitely but not countably additive, exhibits non-conglomerability. This means that there is an event and a countable partition such that is not contained in the interval

To me, all of this suggests that giving up countable additivity is a mistake. We lose some of the most useful and intuitive properties of probability.

For these reasons, I declare finitely additive probability theory to be a lost cause.

Other lost causes I will discuss in the future include fiducial inference and pure likelihood inference. I am tempted to put neural nets into the lost cause category although the recent work on deep learning suggests that may be hasty. Any suggestions?

References

Schervish, Mark, Seidenfeld, Teddy and Kadane, Joseph. (1984). The extent of non-conglomerability of finitely additive probabilities. Zeitschrift f\”{u}r Wahrscheinlichkeitstheorie und Verwandte Gebiete, Volume 66, pp 205-226.

Streater, R. (2007). Lost Causes in and Beyond Physics. Springer.

SIMPSON’S PARADOX EXPLAINED

SIMPSON’S PARADOX EXPLAINED

Imagine a treatment with the following properties:

The treatment is good for men	(E1)
The treatment is good for women	(E2)
The treatment bad overall	(E3)

That’s the essence of Simpson’s paradox. But there is no such treatment. Statements (E1), (E2) and (E3) cannot all be true simultaneously.

Simpson’s paradox occurs when people equate three probabilistic statements (P1), (P2), (P3) described below, with the statements (E1), (E2), (E3) above. It turns out that (P1), (P2), (P3) can all be true. But, to repeat: (E1), (E2), (E3) cannot all be true.

The paradox is NOT that (P1), (P2), (P3) are all true. The paradox only occurs if you mistakenly equate (P1-P3) with (E1-E3).

1. Details

Throughout this post I’ll assume we have essentially an infinite sample size. The confusion about Simpson’s paradox is about population quantities so we needn’t focus on sampling error.

Assume that is binary. The key probability statements are:

	(P1)
	(P2)
	(P3)

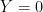Here, is the outcome ( means success, means failure), is treatment (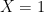 means treated, 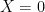means not-treated) and is sex (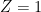 means male, 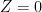means female).

It is easy to construct numerical examples where (P1), (P2) and (P3) are all true. The confusion arises if we equate the three probability statements (P1-P3) with the English sentences (E1-E3).

To summarize: it is possible for (P1), (P2), (P3) to all be true. It is NOT possible for (E1), (E2), (E3) to all be true. The error is in equating (P1-P3) with (E1-E3).

To capture the English statements above, we need causal language, either counterfactuals or causal directed graphs. Either will do. I’ll use counterfactuals. (For an equivalent explanation using causal graphs, see Pearl 2000). Thus, we introduc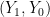e where 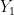is your outcome if treated and is your outcome if not treated. We observe

In other words, if 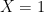we observe 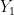and if 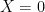we observe . We never observe both 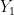and on any person. The correct translation of (E1), (E2) and (E3) is:

	(C1)
	(C2)
	(C3)

These three statements cannot simultaneously be true. Indeed, if the first two statements hold then

Thus, (C1)+(C2) implies (not C3). If the treatment is good for mean and good for women then of course it is good overall.

To summarize, in general we have

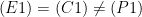
and, moreover (E3) cannot hold if both (E1) and (E2) hold.

The key is that, in general,

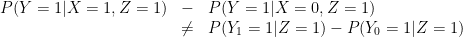
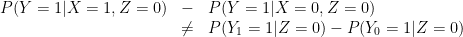
and

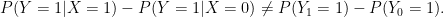
In other words, correlation (left hand side) is not equal to causation (right hand side).

Now, if treatment is randomly assigned, then is independent of and

and so we will not observe the reversal, even for the correlation statements. That is, when is randomly assigned, (P1-P3) cannot all hold.

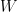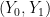In the non-randomized case, we can only recover the causal effect by conditioning on all possible confounding variables . (Recall a confounding variable is a variable that affects both and .) This is because is independent of conditional on 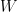(that’s what it means to control for confounders) and we have

and similarly, and so

which reduces the causal effect into a formula involving only observables. This is usually called the adjusted treatment effect. Now, if it should happen that there is only one confounding variable and it happens to be our variable then

In this case we get the correct causal conclusion by conditioning on . That’s why people usually call the conditional answer correct and the unconditional statement misleading. But this is only true if is a confounding variable and, in fact, is the only confounding variable.

2. What’s the Right Answer?

Some texts make it seem as if the conditional answers (P2) and (P3) are correct and (P1) is wrong. This is not necessarily true. There are several possibilities:

1. is a confounder and is the only confounder. Then (P3) is misleading and (P1) and (P2) are correct causal statements.
2. There is no confounder. Moreover, conditioning on causes confounding. Yes, contrary to popular belief, conditioning on a non-confounder can sometimes cause confounding. (I discuss this more below.) In this case, (P3) is correct and (P1) and (P2) are misleading.

3. is a confounder but there are other unobserved confounders. In this case, none of (P1), (P2) or (P3) are causally meaningful.

Without causal language— counterfactuals or causal graphs— it is impossible to describe Simpson’s paradox correctly. For example, Lindley and Novick (1981) tried to explain Simpson’s paradox using exchangeability. It doesn’t work. This is not meant to impugn Lindley or Novick— known for their important and influential work— but just to point out that you need the right language to correctly resolve a paradox. In this case, you need the language of causation.

3. Conditioning on Nonconfounders

I mentioned that conditioning on a non-confounder can actually create confounding. Pearl calls this 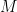-bias. (For those familar with causal graphs, this is bascially the fact that conditioning on a collider creates dependence.)

To elaborate, suppose I want to estimate the causal effect

If is a confounder (and is the only confounder) then we have the identity

that is, the causal effect is equal to the adjusted treatment effect. Let us write

to indicate that the formula for is a function of the distributions and .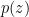

But, if is not a confounder, does the equality still hold? To simplify the discussion assume that there are no other confounders. Either is a confounder or there are no confounders. What is the correct identity for ? Is it

or

The answer (under these assumptions) is this: if is not a confounder then the first identity is correct and if is a confounder then the second identity is correct. In the first case .

Now, when there are no confounders, the first identity is correct. But is the second actually incorrect or will it give the same answer as the first? The answer is: sometimes they gave the same answer but it is possible to construct situations where

(This is something that Judea Pearl has often pointed out.) In these cases, the correct formula for the causal effect is the first one and it does not involve conditioning on . Put simply, conditioning on a non-confounder can (in certain situations) actually cause confounding.

4. Continuous Version

A continuous version of Simpson’s paradox, sometimes called the ecological fallacy, looks like this:

Here we see that increasing doses of drug lead to poorer outcomes (left plot). But when we separate the data by sex () the drug shows better outcomes for higher doses for both males and females.

5. A Blog Argument Resolved?

We saw that in some cases is a function of but in other cases it is only a function of 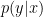. This fact led to an interesting exchange between Andrew Gelman and Judea Pearl and, later, Pearl’s student Elias Bareinboim. See, for example, here and here and here.

As I recall (Warning! my memory could be wrong), Pearl and Bareinboim were arguing that in some cases, the correct formula for the causal effect was the first one above which does not involve conditioning on . Andrew was arguing that conditioning was a good thing to do. This led to a heated exchange.

But I think they were talking past each other. When they said that one should not condition, they meant that the formula for the causal effect does not involve the conditional distribution . Andrew was talking about conditioning as a tool in data analysis. They were each using the word conditioning but they were referring to two different things. At least, that’s how it appeared to me.

6. References

For numerical examples of Simpson’s paradox, see the Wikipedia article.

Lindley, Dennis V and Novick, Melvin R. (1981). The role of exchangeability in inference. The Annals of Statistics, 9, 45-58.

Pearl, J. (2000). Causality: models, reasoning and inference, {Cambridge Univ Press}.

Stephen Ziliak Rejects Significance Testing

In an opinion piece in the Financial Post, Stephen Ziliak goes into the land of hyperbole, declaring that all significance testing is junk science. It starts like this:

I want to believe as much as the next person that particle physicists have discovered a Higgs boson, the so-called “God particle,” one with a mass of 125 gigaelectronic volts (GeV). But so far I do not buy the statistical claims being made about the discovery. Since the claims about the evidence are based on “statistical significance” – that is, on the number of standard deviations by which the observed signal departs from a null hypothesis of “no difference” – the physicists’ claims are not believable. Statistical significance is junk science, and its big piles of nonsense are spoiling the research of more than particle physicists.

He goes on to say:

Statistical significance stinks. In statistical sciences from economics to medicine, including some parts of physics and chemistry, the ubiquitous “test” for “statistical significance” cannot, and will not, prove that a Higgs boson exists, any more than it can prove the reality of God, the existence of a good pain pill, or the validity of loose monetary policy.

While I have said many times in this blog that I, too, think significance testing is mis-used, it is ridiculous to jump to the conclusion that “Statistical significance is junk science.” Ironically, Mr. Ziliak is engaging in exactly the same all-or-nothing thinking that he is criticizing.

You name any statistical method: confidence intervals, Bayesian inference, etc. and it is easy to find people mis-using it. The fact that people mis-use or misunderstand a statistical method does not render it dangerous. The blind and misinformed use of any statistical method is dangerous. Statistical ignorance is the enemy. Mr. Ziliak’s singular focus on the evils of testing seems more cultish than scientific.

Happy Birthday Normal Deviate

Today is the one year anniversary of this blog. First of all, thanks to all the readers. And special thanks to commenters and guest posters. This seems like a good time to assess whether I have achieved my goals for the blog and to get suggestions on how I might proceed in year two.

GOALS. My goals in starting the blog were:

(1) To discuss random things that I happen to find interesting.

(2) To discuss ideas at the interface of statistics and machine learning.

(3) To post every other day.

Goal 1: Achieved.

Goal 2: Partially achieved.

Goal 3: Failed miserably. I was clearly too ambitious. I am lucky if I post once per week.

THE BEST AND WORST. Favorite post: flatland. I still think this is one of the coolest and deepest paradoxes in statistics.

Least Favorite Post: This post where I was dismissive of PAC learning. I think I was just in a bad mood.

LESSON LEARNED. Put “Bayes”, “Frequentist” or “p-value” in the title of a blog post and you get zillions of hits. Put some combination of them and get even more. If I really wanted to get a big readership I would just post exclusively about this stuff. But it would get boring pretty fast.

GOING FORWARD. I hope to keep posting about once per week. But I don’t have any plans to make any specific changes to the blog. I am, however, open to suggestions.

Any suggestions for making the blog more interesting or more fun?

Any suggestions for inducing more people to write comments?

Any topics you would like me to cover? (I already promised to do one on Simpson’s paradox).

The Value of Adding Randomness

In computer science it is common to use randomized algorithms. The same is true in statistics: there are many ways that adding randomness can make things easier. But the way that randomness enters, varies quite a bit in different methods. I thought it might be interesting to collect some specific examples of statistical procedures where added randomness plays some role. (I am not referring to the randomness inherent in the original data but, rather, I refer to randomness in the statistical method itself.)

(1) Randomization in causal inference. The mean difference between a treated group and untreated group is not, in general, equal to the causal effect . (Correlation is not causation.) Moreover, is not identifiable. But if we randomly assign people to the two groups then, magically, . This is easily proved using either the directed graph approach to causation or the counterfactual approach: see here for example. This fact is so elementary that we tend to forget how amazing it is. Of course, this is the reason we spend millions of dollars doing randomized trials.

(As an aside, some people say that there is no role for randomization in Bayesian inference. In other words, the randomization mechanism plays no role in Bayes’ theorem. But this is not really true. Without randomization, we can indeed derive a posterior for but it is highly sensitive to the prior. This is just a restatement of the non-identifiability of . With randomization, the posterior is much less sensitive to the prior. And I think most practical Bayesians would consider it valuable to increase the robustness of the posterior.)

(2) Permutation Tests. If and and you want to test versus , you can get an exact, distribution-free test by using the permutation method. See here. We rarely search over all permutations. Instead, we randomly select a large number of permutations. The result is still exact (i.e. the p-value is sub-uniform under .)

(3) The Bootstrap. I discussed the bootstrap here. Basically, to compute a confidence interval, we approximate the distribution

with the conditional distribution

where , and is a sample from the empirical distribution. But the distribution is intractable. Instead, we approximate it by repeatedly sampling from the empirical distribution function. This makes otherwise intractable confidence intervals trivial to compute.

(4) -means++. Minimizing the objective function in -means clustering is NP-hard. Remarkably, as I discussed here, the -means++ algorithm uses a careful randomization method for choosing starting values and gets close to the minimum with high probability.

(5) Cross-Validation. Some forms of cross-validation involve splitting the data randomly into two or more groups. We use one part(s) for fitting and the other(s) for testing. Some people seem bothered by the randomness this introduces. But it makes risk estimation easy and accurate.

(6) MCMC. An obvious and common use of randomness is random sampling from a posterior distribution, usually by way of Markov Chain Monte Carlo. This can dramatically simplify Bayesian inference.

These are the first few things that came to my mind. Are there others I should add to the list?