2012 in review

The WordPress.com stats helper monkeys prepared a 2012 annual report for this blog.

Here’s an excerpt:

19,000 people fit into the new Barclays Center to see Jay-Z perform. This blog was viewed about 150,000 times in 2012. If it were a concert at the Barclays Center, it would take about 8 sold-out performances for that many people to see it.

Click here to see the complete report.

Big Data at Berkeley

Mike Jordan asked me to post the following information:

The new Simons Institute for the Theory of Computing at Berkeley is an exciting new initiative which will begin organizing semester-long programs starting in 2013.

One of the first programs, set for Fall 2013, will be on the “Theoretical Foundations
of Big Data Analysis”. The organizers of this program are Michael Jordan (chair),
Stephen Boyd, Peter Buehlmann, Ravi Kannan, Michael Mahoney, and Muthu Muthukrishnan.

See http://simons.berkeley.edu/program_bigdata2013.html for more information
on the program.

The Simons Institute has created a number of “Research Fellowships” for young researchers (within at most six years of the award of their PhD) who wish to participate in Institute programs, including the Big Data program. Individuals who already hold postdoctoral positions or who are junior faculty are welcome to apply, as are finishing PhDs.

Please note that the application deadline is January 15, 2013. Further details are available at http://simons.berkeley.edu/fellows.html .

Most Findings Are False

Most Findings Are False

Many of you may know this paper by John Ioannidis called “Why Most Published Research Findings Are False.” Some people seem to think that the paper proves that there is something wrong with significance testing. This is not the correct conclusion to draw, as I’ll explain.

I will also mention a series of papers on a related topic by David Madigan; the papers are referenced at the end of this post. Madigan’s papers are more important than Ioannidis’ papers. Mathbabe has an excellent post about Madigan’s work.

Let’s start with Ioannidis. As the title suggests, the paper claims that many published results are false. This is not surprising to most statisticians and epidemiologists. Nevertheless, the paper has received much attention. Let’s suppose, as Ioannidis does, that “publishing a finding” is synonymous with “doing a test and finding that it is significant.” There are many reasons why published papers might have false findings. Among them are:

1. From elementary probability

   

   In fact, the left hand side can be much larger than the right hand side but it is the quantity on the right hand side that we control with hypothesis testing.

2. Bias. There are many biases in studies so even if the null hypothesis is true, the p-value will not have a Uniform (0,1) distribution. This leads to extra false rejections. There are too many sources of potential bias to list but common ones include: unobserved confounding variables and the tendency to only report studies with small p-values.

These facts are well-known, thus I was surprised that the paper received so much attention. All good epidemiologists know these things and they regard published findings with suitable caution. So, to me, this seems like much ado about nothing. Published findings are considered “suggestions of things to look into,” not “definitive final results.” Nor is this a condemnation of significance testing which is just a tool and, like all tools, should be properly understood. If a fool smashes his finger with a hammer we don’t condemn hammers. (The problem, if there is one, is not testing, but the press, who do report every study as if some definitive truth has been uncovered. But that’s a different story.)

Let me be clear about this: I am not suggesting we should treat every scientific problem as if it is a hypothesis testing problem. And if you have reason to include prior information into an analysis then by all means do so. But unless you have magic powers, simply doing a Bayesian analysis isn’t going to solve the problems above.

Let’s compute the probability of a false finding given that a paper is published. To do so, we will make numerous simplifying assumptions. Imagine we have a stream of studies. In each study, there are only two hypotheses, the null and the alternative . In some fraction of the studies, is true. Let be the event that a study gets published. We do hypothesis testing and we publish just when we reject at level . Assume further that every test has the same power . Then the fraction of published studies with false findings is

It’s clear that can be quite different from . We could recover if we knew ; but we don’t know and just inserting your own subjective guess isn’t much help. And once we remove all the simplifying assumptions, it becomes much more complicated. But this is beside the point because the bigger issue is bias.

The bias problem is indeed serious. It infects any analysis you might do: tests, confidence intervals, Bayesian inference, or whatever your favorite method is. Bias transcends arguments about the choice of statistical methods.

Which brings me to Madigan. David Madigan and his co-workers have spent years doing sensitivity analyses on observational studies. This has been a huge effort involving many people and a lot of work.

They considered numerous studies and asked: what happens if we tweak the database, the study design, etc.? The results, although not surprising, are disturbing. The estimates of the effects vary wildly. And this only accounts for a small amount of the biases that can enter a study.

I do not have links to David’s papers (most are still in review) so I can’t show you all the pictures but here is one screenshot:

Each horizontal line is one study; the dots show how the estimates change as one design variable is tweaked. This picture is just the tip of the iceberg. (It would be interesting to see if the type of sensitivity analysis proposed by Paul Rosenbaum is able to reveal the sensitivity of studies but it’s not clear if that will do the job.)

To summarize: many published findings are indeed false. But don’t blame this on significance testing, frequentist inference or incompetent epidemiologists. If anything, it is bias. But really, it is simply a fact. The cure is to educate people (and especially the press) that just because a finding is published doesn’t mean it’s true. And I think that the sensitivity analysis being developed by David Madigan and his colleagues will turn out to be essential.

References

Ryan, P.B., Madigan, D., Stang, P.E., Overhage, J.M., Racoosin, J.A., Hartzema, A.G. (2012). Empirical Assessment of Analytic Methods for Risk Identification in Observational Healthcare Data: Results from the Experiments of the Observational Medical Outcomes Partnership. Statistics in Medicine, to appear.

Ryan, P., Suchard, M.A., and Madigan, D. (2012). Learning from epidemiology: Interpreting observational studies for the effects of medical products. Submitted.

Schuemie, M.J., Ryan, P., DuMouchel, W., Suchard, M.A., and Madigan, D. (2012). Significantly misleading: Why p-values in observational studies are wrong and how to correct them. Submitted.

Madigan, D., Ryan, P., Schuemie, M., Stang, P., Overhage, M., Hartzema, A., Suchard, M.A., DuMouchel, W., and Berlin, J. (2012). Evaluating the impact of database heterogeneity on observational studies.

Guest Post: ROB TIBSHIRANI

GUEST POST: ROB TIBSHIRANI

Today we have a guest post by my good friend Rob Tibshirani. Rob has a list of nine great statistics papers. (He is too modest to include his own papers.) Have a look and let us know what papers you would add to the list. And what machine learning papers would you add? Enjoy.

9 Great Statistics papers published after 1970
Rob Tibshirani

I was thinking about influential and awe-inspiring papers in Statistics and thought it would be fun to make a list. This list will show my bias in favor of practical work, and by its omissions, my ignorance of many important subfields of Statistics. I hope that others will express their own opinions.

1. Regression models and life tables (with discussion) (Cox 1972). A beautiful and elegant solution to an extremely important practical problem. Has had an enormous impact in medical science. David Cox deserves the Nobel Prize in Medicine for this work.
2. Generalized linear models (Nelder and Wedderburn 1972). Formulated the class of generalized regression models for exponential family distributions. Provided the framework for the {\tt glim} package and the S and R modelling languages.
3. Maximum Likelihood from Incomplete Data via the {EM} Algorithm (with discussion) (Dempster, Laird, and Rubin 1977). Brought together many related ideas for dealing with missing or messy data, in one conceptually simple and powerful framework.
4. Bootstrap methods: another look at the jackknife (Efron 1979). Introduced one of the first computer-intensive statistical tools. Widely used in many scientific fields
5. Classification and regression trees (Breiman, Friedman, Olshen and Stone 1984). Not a paper, but a book. Among the first proposals for data mining to demonstrate the power of a detailed practical implementation of a method, including cross-validation for model selection
6. How biased is the error rate of a prediction rule? (Efron 1986). Greatly advanced our understanding of training and test error rates, and overfitting and ways to deal with them.
7. Sampling based approaches to calculating marginal densities (Gelfand and Smith 1990). Buidling on earlier work by Geman and Geman, Tanner and Wong, and others, this paper developed a simple and elegant sampling-based method for estimating marginal densities. Huge impact on Bayesian work
8. Controlling the false discovery rate: a practical and powerful approach to multiple testing (Benjamini and Hochberg 1995). Introduced the FDR and a selection procedure whose FDR is controlled at a given level. Enormously influential in the modern age of high-dimensional data.
9. A decision-theoretic generalization of online learning and an application to boosting (Freund and Schapire 1995). Not a statistics paper per se, but one that introduced one of the most powerful supervised learning methods and changed the way that many of us thought about the prediction problem.

Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B., 85, 289-300.

Breiman, L. and Friedman, J. and Olshen, R. and Stone, C. (1984). Classification and Regression Trees, Wadsworth, New York.

Cox, D.R. (1972). Regression models and life tables (with discussion). J. Royal. Statist. Soc. B., 74, 187-220.

Dempster, A., Laird, N and Rubin, D. (1977). Maximum Likelihood from Incomplete Data via the {EM} Algorithm (with discussion). Journal of the Royal Statistical Society Series B, 39, 1-38.

Efron, B. (1979). Bootstrap methods: another look at the jackknife. Annals of Statistics, 7, 1-26.

Efron, B. (1986). How biased is the apparent error rate of a prediction rule? Journal of the American Statistical Association, 81, 461-470.

Freund, Y. and Schapire, R. (1997). A decision-theoretic generalization of online learning and an application to boosting. Journal of Computer and System Sciences, 55, 119-139.

Gelfand, A. and Smith, A. (1990). Sampling based approaches to calculating marginal densities. Journal of the American Statistical Association, 85, 398-409.

Nelder, J.A. and Wedderburn, R.W. (1972). Generalized linear models. J. Royal Statist. Soc. B., 135, 370-384.

New Names For Statistical Methods

Statisticians and Computer Scientists have done a pretty poor job of thinking of names for procedures. Names are important. No one is going to use a method called “the Stalin-Mussolini Matrix Completion Algorithm.” But who would pass up the opportunity to use the “Schwarzenegger-Shatner Statistic.” So, I have decided to offer some suggestions for re-naming some of our procedures. I am open to further suggestions.

Bayesian Inference. Bayes did use his famous theorem to do a calculation. But it was really Laplace who systematically used Bayes’ theorem for inference.
New Name: Laplacian Inference.

Bayesian Nets. A Bayes nets is just a directed acyclic graph endowed with probability distribution. This has nothing to do with Bayesian — oops, I mean Laplacian — inference. According to Wikipedia, it was Judea Pearl who came up with the name.
New Name: Pearl Graph.

The Bayes Classification Rule. Give , with , the optimal classifier is to guess that when and to guess that when . This is often called the Bayes rule. This is confusing for many reasons. Since this rule is a sort of gold standard how about:
New Name: The Golden Rule.

Unbiased Estimator. Talk about a name that promises more than it delivers.
New Name: Mean Centered Estimator.

Credible Set. This is a set with a specified posterior probability content such as: here is a 95 percent credible set. Might as well make it sound more exciting.
New Name: Incredible Set.

Confidence Interval. I am tempted to suggest “Uniform Frequency Coverage Set” but that’s clumsy. However it does yield a good acronym if you permute the letter a bit.
New Name: Coverage Set.

The Bootstrap. If I remember correctly, Brad Efron considered several names and John Tukey suggested “the shotgun.” Brad, you should have listened to Tukey.
New Name: The Shotgun.

Causal Inference. For some reason, whenever I try to type “causal” I end up typing “casual.” Anyway, the mere mention of causation upsets some people. Some people call causal inference “the analysis of treatment effects” but that’s boring. I suggest we go with the opposite of casual:
New Name: Formal Inference.

The Central Limit Theorem. Boring! For historical reasons I suggest:
de Moivre’s Theorem.

The Law of Large Numbers. Another boring name. Again, to respect history I suggest:
New Name: Bernoulli’s Theorem.

Minimum Variance Unbiased Estimator. Let’s just eliminate this one.

The lasso. Nice try Rob, but most people don’t even know what it stands for. How about this:
New Name: the Taser. (Tibshirani’s Awesome Sparse Estimator for regression).

Stigler’s law of eponymy. If you don’t know what this is, check it out on Wikipedia. The you’ll understand why it name should be:
New Name: Stigler’s law of eponymy.

Neural nets. Let’s call them what they are.
(Not so) New name: Nonlinear regression.

p-values. I hope you’ll agree that this is a less than inspiring name. The best I can come up with is:
New Name: Fisher Statistic.

Support Vector Machines. This might get the award for the worst name ever. Sounds like some industrial device in a factory. Since we already like the acronym VC, I suggest:
New Name: Vapnik Classifier.

U-statistic. I think this one is obvious.
New Name: iStatistic.

Kernels. In statistics, this refers to a type of local smoothing, such as kernel density estimation and Nadaraya-Watson kernel regression. Some people use “Parzen Window” which sounds like something you buy when remodeling your house. But in Machine Learning it is used to refer to Mercer kernels with play a part in Reproducing Kernel Hilbert Spaces. We don’t really need new names we just need to clarify how we use the terms:
New Usage: Smoothing Kernels for density estimators etc. Mercer kernels for kernels that generate a RKHS.

Reproducing Kernel Hilbert Space. Saying this phrase is exhausting. The acronym RKHS is not much better. If we used history as a guide we’d say Aronszajn-Bergman space but that’s just as clumsy. How about:
New Name: Mercer Space.

0. No constant is used more than 0. Since no one else has ever names it, this is my chance for a place in history.
New Name: Wasserman’s Constant.

FLAT PRIORS IN FLATLAND: STONE’S PARADOX

FLAT PRIORS IN FLATLAND: STONE’S PARADOX

Mervyn Stone is Emeritus Professor at University College London. He is famous for his work on Bayesian inference as well as pioneering work on cross-validation, coordinate-free multivariate analysis, as well as many other topics.

Today I want to discuss a famous example of his, described in Stone (1970, 1976, 1982). In technical jargon, he shows that “a finitely additive measure on the free group with two generators is nonconglomerable.” In English: even for a simple problem with a discrete parameters space, flat priors can lead to surprises. Fortunately, you don’t need to know anything about free groups to understand this example.

1. Hunting For a Treasure In Flatland

I wonder randomly in a two dimensional grid-world. I drag an elastic string with me. The string is taut: if I back up, the string leaves no slack. I can only move in four directions: North, South, West, East.

I wander around for a while then I stop and bury a treasure. Call the path . Here is an example:

Now I take one more random step. Each direction has equal probability. Call the final path . So it might look like this:

Two people, Bob (a Bayesian) and Carla (a classical statistician) want to find the treasure. There are only four possible paths that could have yielded , namely:

Let us call these four paths N, S, W, E. The likelihood is the same for each of these. That is, 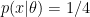for 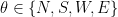. Suppose Bob uses a flat prior. Since the likelihood is also flat, his posterior is

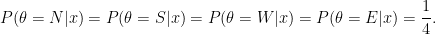
Let 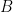be the three paths that extend . In this example, . Then .

Now Carla is very confident and selects a confidence set with only one path, namely, the path that shortens . In other words, Carla’s confidence set is .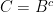

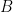Notice the following strange thing: no matter what is, Carla gets the treasure with probability 3/4 while Bob gets the treasure with probability 1/4. That is, but the coverage of is 1/4. In other words, for every . On the other hand, the coverage of 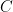is 3/4: for every .

Here is quote from Stone (1976): (except that I changed his B and C to Bob and Carla):

“ … it is clear that when Bob and Carla repeatedly engage in this treasure hunt, Bob will find that his posterior probability assignment becomes increasingly discrepant with his proportion of wins and that Carla is, somehow, doing better than [s]he ought. However, there is no message … that will allow Bob to escape from his Promethean situation; he cannot learn from his experience because each hunt is independent of the other.”

2. More Trouble For Bob

Let be the event that the final step reduces the length of the string. Using his posterior distribution, Bob finds that for each . Since this holds for each , Bob deduces that .

On the other hand, Bob notes that for every . Hence, .

Bob has just proved that .

3. The Source of The Problem

The apparent contradiction stems from the fact that the prior is improper. Technically this is an example of the non-conglomerability of finitely additive measures. For a rigorous explanation of why this happens you should read Stone’s papers. Here is an abbreviated explanation, from Kass and Wasserman (1996, Section 4.2.1).

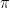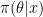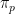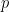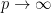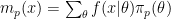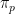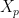Let denotes Bob’s improper flat prior and let denote his posterior distribution. Let denote the prior that is uniform on the set of all paths of length . This is of course a proper prior. For any fixed , as . So Bob can claim that his posterior distribution is a limit of well-defined posterior distributions. However, we need to look at this more closely. Let be the marginal of induced by . Let denote all ‘s of length 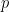or . When , is a poor approximation to 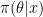since the former is concentrated on a single point while the latter is concentrated on four points. In fact, the total variation distance between and 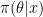is 3/4 for . 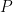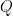(Recall that the total variation distance between two probability measures and is 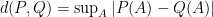.) Furthermore, 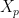is a set with high probability: as .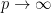

While converges to 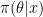as 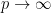for any fixed , they are not close with high probability.

This problem disappears if you use a proper prior.

4. The Four Sided Die

Here is another description of the problem. Consider a four sided die whose sides are labeled with the symbols 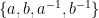. We roll the die several times and we record the label on the lowermost face (there is a no uppermost face on a four-sided die). A typical outcome might look like this string of symbols:

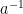Now we apply an annihilation rule. If and appear next to each other, we eliminate these two symbols. Similarly, if and appear next to each other, we eliminate those two symbols. So the sequence above gets reduced to:

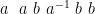
Let us denote the resulting string of symbols, after removing annihilations, by . Now we toss the die one more time. We add this last symbol to and we apply the annihilation rule once more. This results in a string which we will denote by .

You get to see and you want to infer .

Having observed , there are four possible values of and each has the same likelihood. For example, suppose 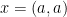. Then has to be one of the following:

The likelihood function is constant over these four values.

Suppose we use a flat prior on . Then the posterior is uniform on these four possibilities. Let denote the three values of that are longer than . Then the posterior satisfies

Thus is a 75 percent posterior confidence set.

However, the frequentist coverage of is 1/4. To see this, fix any . Now note that contains if and only if concatenated with is smaller than . This happens only if the last symbol is annihilated, which occurs with probability 1/4.

5. Likelihood

Another consequence of Stone’s example is that, in my opinion, it shows that the Likelihood Principle is bogus. According to the likelihood principle, the observed likelihood function contains all the useful information in the data. In this example, the likelihood does not distinguish the four possible parameter values.

But the direction of the string from the current position — which does not affect the likelihood — clearly has lots of information.

6. Proper Priors

If you want to have some fun, try coming up with proper priors on the set of paths. Then simulate the example, find the posterior and try to find the treasure.

Better yet, have a friend simulate the a path. Then you choose a prior, compute the posterior and guess where the treaure is. Repeat the game many times. Your friend generates a different path every time. If you try this, I’d be interested to hear about the simulation results.

Another question this example raises is: should we ever use improper priors? Flat priors that do not have mass can be interpreted as finitely additive priors. The father of Bayesian inference, Bruno DeFinetti, was adamant in rejecting the axiom of countable additivity. He thought flat priors like Bob’s were fine.

It seems to me that in modern Bayesian inference, there is not universal agreement on whether flat priors are evil or not. In some cases they work fine in others they don’t. For example, poorly chosen improper priors in random effects models can lead to improper (non-integrable) posteriors. But other improper priors don’t cause this problem.

In Stone’s example I think that most statisticians would reject Bob’s flat prior-based Bayesian inference.

7. Conclusion

I have always found this example to be interesting because it seems very simple and, at least at first, one doesn’t expect there to be a problem with using a flat prior. Technically the problems arise because there is group structure and the group is not amenable. Hidden beneath this seemingly simple example is some rather deep group theory.

Many of Stone’s papers are gems. They are not easy reading (with the exception of the 1976 paper) but they are worth the effort.

8. References

Stone, M. (1970). Necessary and sufficient condition for convergence in probability to invariant posterior distributions. The Annals of Mathematical Statistics, 41, 1349-1353,

Stone, M. (1976). Strong inconsistency from uniform priors. Journal of the American Statistical Association, 71, 114-116.

Stone, M. (1982). Review and analysis of some inconsistencies related to improper priors and finite additivity. Studies in Logic and the Foundations of Mathematics, 104, 413-426.

Kass, R.E. and Wasserman, L. (1996). The selection of prior distributions by formal rules. Journal of the American Statistical Association, 91, 1343-1370.

Nate Silver is a Frequentist: Review of “the signal and the noise”

Nate Silver Is A Frequentist
Review of “the signal and the noise” by Nate Silver

There are not very many self-made statisticians, let alone self-made statisticians who become famous and get hired by the New York Times. Nate Silver is a fascinating person. And his book the signal and the noise, is a must read for anyone interested in statistics.

The book is about prediction. Silver chronicles successes and failures in the art of prediction and he does so with clear prose and a knack for good storytelling.

Along the way, we learn about his unusual life path. He began as an economic consultant for KPMG. But his real passion was predicting player performance in baseball. He developed PETOCA, a statistical baseball analysis system which earned him a reputation as a crack forecaster. He quit his day job and made a living playing online poker. Then he turned to political forecasting, first at the Daily Kos and later at his own website, FiveThirtyEight.com. His accurate predictions drew media attention and in 2010 he became a blogger and writer for the New York Times.

The book catalogues notable successes and failures in prediction. The first topic is the failure of ratings agencies to predict the bursting of the housing bubble. Actually, the bursting of the bubble was predicted, as Silver points out. The problem was that Moody’s and Standard and Poor’s either ignored or downplayed the predictions. He attributes to failure to having too much confidence in their models and not allowing for outliers. Basically, he claims, they confused good “in-sample prediction error” as being the same as “good out-of-sample prediction error.”

Next comes a welcome criticism of bogus predictions from loud-mouthed pundits on news shows. Then, a fun chapter on how he used relatively simple statistical techniques to become a crackerjack baseball predictor. This is a theme that Silver touches on several times. If you can find a field that doesn’t really on statistical techniques, you can become a star just by using some simple, common sense methods. He attributes his success at online poker, not to his own acumen, but to the plethora of statistical dolts who were playing online poker at the time.

He describes weather forecasting as a great success detailing the incremental, painstaking improvements that have taken place over many years.

One of the striking facts about the book is the emphasis the Silver places on frequency calibration. (I’ll have more to say on this shortly.) He draws a plot of observed frequency versus forecast probability for the National Weather Service. The plot is nearly a straight line. In other words, of the days that the Weather Service said there was a 60 percent chance of raining, it rained 60 percent of the time.

Interestingly, the calibration plot for the Weather Channel shows a bias at the lower frequencies. Apparently, this is intentional. The loss function for the Weather Channel is different than the loss function for the Nation Weather Service. The latter wants accurate (calibrated) forecasts. The Weather Channel wants accuracy too, but they also want to avoid making people annoyed. It is in their best interests to over-predict rain slightly for obvious reasons: if they predict rain and it turns out to be sunny, no big deal. But if they predict sunshine and it rains, people get mad.

Next come earthquake predictions and economic predictions. He rates both as duds. He goes on to discuss epidemics, chess, gambling, the stock market, terrorism, and climatology. When discussing the accuracy of climatology forecasts he is way too forgiving (a bit of political bias?). More importantly, he ignores the fact that developing good climate policy inevitably involves economic prediction, to which he already gave a failing grade. (Is it better to spend a trillion dollars helping Micronesia develop a stronger economy so they don’t rely so much on farming close to the shore, or to spend the money on reducing carbon output and hence delay rising sea levels by two years? Climate policy is inextricably tied to economics.)

Every chapter has interesting nuggets. I especially liked the chapter on computer chess. I knew that Deep Blue beat Gary Kasparov but beyond that, I didn’t know much. The book gives lots of juicy details.

As you can see, I liked the book very much and I highly recommend it.

But …

I have one complaint. Silver is a big fan of Bayesian inference, which is fine. Unfortunately, he falls into that category I referred to a few posts ago. He confuses “Bayesian inference” with “using Bayes’ theorem.” His description of frequentist inference is terrible. He seems to equate frequentist inference with Fisherian significance testing, most using Normal distributions. Either he learned statistics from a bad book or he hangs out with statisticians with a significant anti-frequentist bias.

Have no doubt about it: Nate Silver is a frequentist. For example, he says:

“One of the most important tests of a forecast — I would argue that it is the single most important one — is called calibration. Out of all the times you said there was a 40 percent chance of rain, how often did rain actually occur? If over the long run, it really did rain about 40 percent of the time, that means your forecasts were well calibrated.”

It does not get much more frequentist than that. And if using Bayes’ theorem helps you achieve long run frequency calibration, great. If it didn’t, I have no doubt he would have used something else. But his goal is clearly to have good long run frequency behavior.

This theme continues throughout the book. Here is another quote from Chapter 6:

“A 90 percent prediction interval, for instance, is supposed to cover 90 percent of the possible real-world outcomes, … If the economists’ forecasts were as accurate as they claimed, we’d expect the actual value for GDP to fall within their prediction interval nine times out of then …”

That’s the definition of frequentist coverage. In Chapter 10 he does some data analysis on poker. He uses regression analysis with some data-splitting. No Bayesian stuff here.

I don’t know if any statisticians proof-read this book but if they did, it’s too bad they didn’t clarify for Silver what Bayesian inference and frequentist inference really are.

But perhaps I am belaboring this point too much. This is meant to be a popular book, after all, and if it helps to make statistics seem cool and important, then it will have served an important function.

So try not to be as pedantic as me when reading the book. Just enjoy it. I used to tell people at parties that I am an oil-fire fighter. Now I’ll say: “I’m a statistician. You know. Like that guy Nate Silver.” And perhaps people won’t walk away.

Screening and False Discovery Rates

Today we have another guest post. This one is by Ryan Tibshirani an Assistant Professor in my department. (You might also want to check out the course on Optimization that Ryan teaches jointly with Geoff Gordon.)

Screening and False Discovery Rates
by Ryan Tibshirani

Two years ago, as a TA for Emmanuel Candes’ Theory of Statistics course at Stanford University, I posed a question about screening and false discovery rates on a class homework. Last year, for my undergraduate Data Mining course at CMU, I re-used the same question. The question generated some interesting discussion among the students, so I thought it would be fun to share the idea here. Depending on just how popular Larry’s blog is (or becomes), I may not be able to use it again for this year’s Data Mining course! The question is inspired by conversations at the Hastie-Tibs-Taylor group meetings at Stanford.

Consider a two class problem, genetics inspired, with people and gene expression measurements. The people are divided into two groups: are healthy, and are sick. We have null genes (in which there is actually no underlying difference between healthy and sick patients), and non-nulls (in which there actually is a difference). All measurements are independent.

Suppose that we compute a two sample -statistic for each gene . We want to call some genes significant, by thresholding these -statistics (in absolute value); we then want to estimate the false discovery rate (FDR) of this thresholding rule, which is

The Benjamini-Hochberg (BH) procedure provides a way to do this, which is best explained using the -values from , respectively. We first sort the -values ; then, given a level , we find the largest such that

and call the -values (and the corresponding genes) significant. It helps to think of this as a rule which rejects all -values satisfying , for the cutoff . The BH estimate for the FDR of this rule is simply .

An alternative procedure to estimate the FDR uses a null distribution generated by permutations. This means scrambling all of the group labels (healthy/sick) uniformly at random, and then recomputing the -statistics. Having done this times, we let denote the -statistics computed on the th permuted data set. Now consider the rule that rejects all -statistics satisfying for some cutoff . The permutation estimate for the FDR of this rule is

How good are these estimates? To answer this, we’ll look at a simulated example, in which we know the true FDR. Here we have patients and genes, of which are null. The gene expression measurements are all drawn independently from a standard normal distribution with mean zero, except for the non-null genes, where the mean was chosen to be -1 or 1 (with equal probability) for the sick patients. The plot below shows the estimates as we vary the cutoff (for the BH procedure, this means varying the level ) versus the true FDR, averaged over 10 simulated data sets. Both estimates look quite accurate, with the BH estimate being a little conservative.

Now what happens if, before computing these estimates, we restricted our attention to a small group of genes that looked promising in the first place? Specifically, suppose that we screened for genes based on high between-group variance (between the healthy and sick groups). The idea is to only consider the genes for which there appears to a difference between the healthy and sick groups. Turning to our simluated example, we kept only 1000 of the 2000 genes with the highest between-group variance, and then computed the BH and permutation estimates as usual (as if we were given this screened set to begin with). The plot below shows that the FDR estimates are now quite bad, as they’re way too optimistic.

Here is the interesting part: if we screen by total variance (the variance of all gene expression measurements, pooling the healthy and sick groups), then this problem goes away. The logic behind screening by total variance is that, if there’s not much variability overall, then there’s probably no interesting difference between the healthy and sick groups. In our simulated example, we kept only 1000 of the 2000 genes with the highest total variance, and computed the BH and permutation estimates as usual. We can see below that both estimates of the FDR are actually pretty much as accurate as they were in the first place (with no screening performed), if not a little more conservative.

Why do you think that the estimates after screening by between-group variance and by total variance exhibit such different behaviors? I.e., why is it OK to screen by total variance but not by between-group variance? I’ll share my own thoughts in a future post.