P-values Gone Wild and Multiscale Madness

I came across a very interesting paper by E. J. Masicampo and Daniel Lalande called A peculiar prevalence of p values just below .05. The link is here. (I saw it referenced at marginal revolution.

1. Peculiar Prevalence

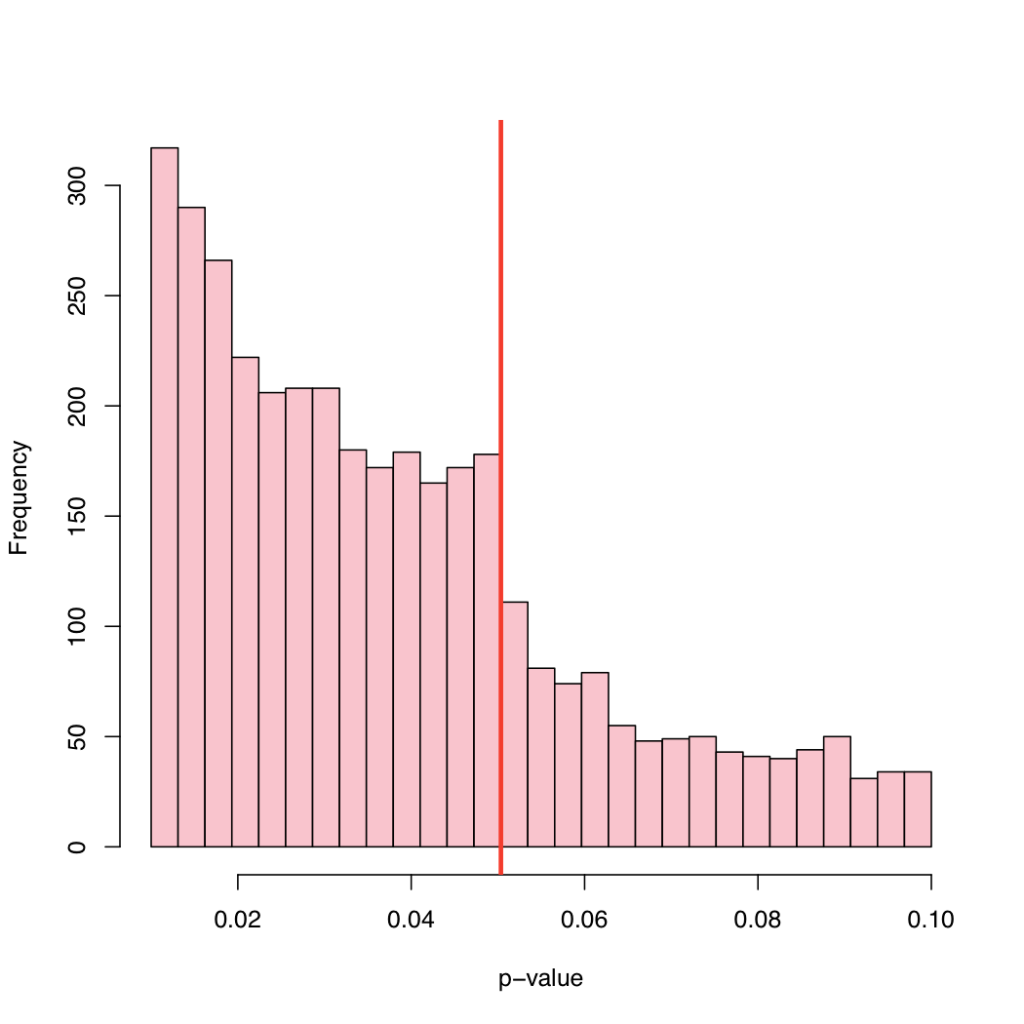
I recommend reading the paper to get the full details. The quick summary is that they collected 3,627 p-values from journals. They found a statistical anomaly in the form of an excess just below 0.05. (They fit a parametric distribution to the p-values and demonstrated a significant departure right below 0.05).

There are some obvious explanations. First, selection bias. Studies with p-values above 0.05 are less likely to be published. Second, the tweaking effect. If you do a study and get a p-value just above .05 you might be tempted to tweak the analysis a bit until you get the p-value just below 0.05. I am not suggesting malfeasance. This could be done quite subconsciously.

You might say: well I would have predicted this would happen anyway. Perhaps. But it is quite interesting to see a carefully done study document and quantify the effect.

E.J. Masicampo was kind enough to share the data with me. Here is a histogram of the p-values.

The jump just below 0.05 is quite noticeable.

2. Multiscale Madness

Now I want to raise a meta-statistical issue. Fitting a parametric model and looking for a big residual is certainly a reasonable approach. But can we do this nonparametrically?

The density of p-values is a mixture of the form

\displaystyle h(p) = (1-\pi) u(p) + \pi g(p)

where {\pi} is the fraction of non-null effects, {u(p)=1} is the uniform density (the density of {p} under the null) and {g(p)} is the density of p-values for the non-null effects. The unknowns are {\pi} and {g(p)}. It is not unrealistic to assume that {g(p)} is decreasing. This implies that {h} is some decreasing density.

So, statistically, we might want to look for suspicious non-decreasing parts of the density. A good tool for doing this is the distribution free method developed in Dumbgen and Walther (2008). Briefly, the idea is this.

Consider data {X_1,\ldots, X_n} from a density {h}. Let

\displaystyle X_{(1)} \leq \cdots \leq X_{(n)}

be the order statistics. Now construct all the local order statistics

\displaystyle \frac{X_{(i)}-X_{(j)}}{X_{(k)}-X_{(j)}}

for {j \leq i \le k}. These local order statistics are combined into a multiscale test statistic {T_{jk}}. Then we find the set of intervals

\displaystyle {\cal D}^+ = \{ (X_{(j)},X_{(k)}):\ T_{jk} > c_{jk}(\alpha)\}

which are the intervals where the density apparently increases. It is possible to explicitly calculate the critical values {c_{jk}(\alpha)} . One can then claim that all the intervals in {{\cal D}^+} must have an increase in the density {h}. The probability that this claim is wrong as at most {\alpha}. This procedure is exact: it is finite sample and distribution free. (Of course, one can construct intervals of decrease as well but for our problem, {{\cal D}^+} is the set of interest.)

The procedure is implemented in the R package modehunt, written by Kaspar Rufibach and Guenther Walther. When applied to the p-values (I am ignoring a small technical issue, namely, that the data are rounded) we get the following:

The horizontal lines show the intervals with apparent increases in the density. The result confirms the findings of Masicampo and Lalande. There seems to be suspicious increases just below 0.05.

To quote Arte Johnson,
Verrry Interesting!

3. References

Dumbgen, L. and Walther, G. (2008). Multiscale Inference about a density. The Annals of Statistics, 36, 1758–1785.

Masicampo, E.J. and Lalande, D. (2012). A peculiar prevalence of p values just below .05. The Quarterly Journal of Experimental Psychology. http://www.tandfonline.com/doi/abs/10.1080/17470218.2012.711335.

—Larry Wasserman

This entry was written by normaldeviate, posted on August 16, 2012 at 6:15 pm, filed under Uncategorized. Bookmark the permalink. Follow any comments here with the RSS feed for this post. Both comments and trackbacks are currently closed.

15 Comments

  1. E. J. Masicampo
    Posted August 16, 2012 at 8:58 pm | Permalink

    Very cool, Larry. Thanks for sharing this!

  2. apwheele
    Posted August 16, 2012 at 9:44 pm | Permalink

    This has been receiving a lot of press lately, I will need to read both more closely, but to those interested another article currently on SSRN does a similar analysis of p-values in top economic journals, . Their histograms look at z-statistics instead of p-values though, so off-the-cuff I can’t tell if the distribution of tests are similar (from the abstract(s) their findings appear to be largely the same though).

    Brodeur et al., 2012. Star Wars: The Empirics Strike Back

  3. Nathaniel Beck
    Posted August 17, 2012 at 11:01 am | Permalink

    Same p value finding (absense of p between .05 and .10 or so) found in pol sci by gerber and malhotra. My guess is that anyone with a computer who starts with p under .1 can respecify to hit the magic .05 without effort – since i know we can always get a result with at least one magic star i propose all stats programs do that automatically (much easier than looking at posterior densities).

  4. kenmccue
    Posted August 18, 2012 at 7:10 pm | Permalink

    I thought you were opposed to mixture models. Tequila or some such comparison.

  5. JJ
    Posted September 25, 2012 at 10:50 am | Permalink

    I don’t understand why p-values between 0.045 and 0.05 have higher residuals and not p-values between 0.05 and 0.055. If scientists are tweaking their p-values, they should make the p-values just above 0.05 disappear… This does not appear in the graph. Other interpretation is that all p-values between 0.05 and 0.1 are under-represented because people don’t publish them. What do you think?

    • normaldeviate
      Posted September 25, 2012 at 11:26 am | Permalink

      The plot only shows regions where the density is higher than expected

      • JJ
        Posted September 25, 2012 at 6:05 pm | Permalink

        Yes, but in the original paper, the frequency of p-values between 0.05 and 0.1 are shown and there is no deep in frequencies for p-values between 0.05 and 0.055.

  6. Paulo.
    Posted October 1, 2012 at 1:35 pm | Permalink

    Hi Larry, since you have their data set, can you check if the most significant (leading) digit of the p-values is approximately Benford distributed?

  7. xi'an
    Posted October 2, 2012 at 1:51 am | Permalink

    Interesting histogram and pont! I however wonder at the rationale for looking for a uniform component in the mixture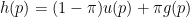 \displaystyle h(p) = (1-\pi) u(p) + \pi g(p) as (a) those p-values are presumably about different models and observations (so no frequentist argument there) and (b) there are so many selection biases in the selection of those p-values that there is no rationale for having a part of them distributed as a uniform “under the null”. Not that your test uses this uniform component anyway…

  8. László Sándor
    Posted October 11, 2012 at 4:08 pm | Permalink

    I would be interested in a different application of this logic, if you think it is reasonable. In the recent literature of public finance (or any micro-empirical economics) bunching is in fashion as a nonparametric measure of responsiveness where marginal incentives change. (Primary example: Entering a new tax bracket.)

    I wonder if you have thoughts on an appealing statistical model of the phenomenon, with a null of no response only noise, and testing. (And of course confidence intervals.) What you did for p-values is not what the pioneers of the approach did for earnings so far. If you have time to skim two pieces, here are the main ones:

    Click to access saezAEJ10bunching.pdf

    Click to access denmark_adjcost.pdf

    Thanks!

4 Trackbacks

  1. By A peculiar prevalence of p values just below .05 « Epanechnikov's Blog on August 17, 2012 at 8:23 am

    […] More here and here. […]

  2. By The “p” stands for “perplexing” » Source-Filter on August 25, 2012 at 11:42 am

    […] read about this paper at wmbriggs.com first. Then I saw the post at Normal Deviate, which presents an interesting non-parametric treatment of the data (the non-parametric results […]

  3. By Null Results » Duck of Minerva on January 16, 2013 at 10:02 am

    […] If we really care about truth-seeking in the social sciences, let alone our own discipline of political science, we would consider null results on significant issues of critical importance. We would certainly consider them more important than the far-too-common paper with a  ”positive” result that results from, well, efforts to get to a positive result via “tweaking” (e.g., and, also). […]

  4. By Friday links: significant excess of (barely) significant results, sympathy for the dean, and more | Dynamic Ecology on August 30, 2013 at 7:31 am

    […] but good: I missed this at the time, but Larry Wasserman of Normal Deviate discusses an interesting study showing that, in each of three leading psychology journals, published papers […]