Robins and Wasserman Respond to a Nobel Prize Winner
James Robins and Larry Wasserman
Note: This blog post is written by two people and it is cross-posted at Normal Deviate and Three Toed Sloth.
Chris Sims is a Nobel prize winning economist who is well known for his work on macroeconomics, Bayesian statistics, vector autoregressions among other things. One of us (LW) had the good fortune to meet Chris at a conference and can attest that he is also a very nice guy.
Chris has a paper called On an An Example of Larry Wasserman. This post is a response to Chris’ paper.
The example in question is actually due to Robins and Ritov (1997). A simplified version appeared in Wasserman (2004) and Robins and Wasserman (2000). The example is related to ideas from the foundations of survey sampling (Basu 1969, Godambe and Thompson 1976) and also to ancillarity paradoxes (Brown 1990, Foster and George 1996).
1. The Model
Here is (a version of) the example. Consider iid random variables
The random variables take values as follows:
Think of as being very, very large. For example,
and
.
The idea is this: we observe . Then we flip a biased coin
. If
then you get to see
. If
then you don’t get to see
. The goal is to estimate
Here are the details. The distribution takes the form
Note that and
are independent, given
. For simplicity, we will take
to be uniform on
. Next, let
where is a function. That is,
. Of course,
Similarly, let
where is a function. That is,
. Of course,
The function is known. We construct it. Remember that
is the probability that we get to observe
given that
. Think of
as something that is expensive to measure. We don’t always want to measure it. So we make a random decision about whether to measure it. And we let the probability of measuring
be a function
of
. And we get to construct this function.
Let be a known, small, positive number. We will assume that
for all .
The only thing in the the model we don’t know is the function . Again, we will assume that
Let denote all measurable functions on
that satisfy the above conditions. The parameter space is the set of functions
.
Let be the set of joint distributions of the form
where , and
and
satisfy the conditions above. So far, we are considering the sub-model
in which
is known.
The parameter of interest is . We can write this as
Hence, is a function of
. If we know
then we can compute
.
2. Frequentist Analysis
The usual frequentist estimator is the Horwitz-Thompson estimator
It is easy to verify that is unbiased and consistent. Furthermore,
. In fact, let us define
where
It follows from Hoeffding’s inequality that
Thus we have a finite sample, confidence interval with length
.
Remark: We are mentioning the Horwitz-Thompson estimator because it is simple. In practice, it has three deficiencies:
- It may exceed 1.
- It ignores data on the multivariate vector
except for the one dimensional summary
.
- It can be very inefficient.
These problems are remedied by using an improved version of the Horwitz-Thompson estimator. One choice is the so-called locally semiparametric efficient regression estimator (Scharfstein et al., 1999):
where ,
are basis functions, and
are the mle’s (among subjects with
) in the model
Here can increase slowly with
Recently even more efficient estimators have been derived. Rotnitzky et al (2012) provides a review. In the rest of this post, when we refer to the Horwitz-Thompson estimator, the reader should think “improved Horwitz-Thompson estimator.” End Remark.
3. Bayesian Analysis
To do a Bayesian analysis, we put some prior on
. Next we compute the likelihood function. The likelihood for one observation takes the form
. The reason for having
in the exponent is that, if
, then
is not observed so the
gets left out. The likelihood for
observations is
where we used the fact that . But remember,
is known. In other words,
is known. So, the likelihood is
Combining this likelihood with the prior creates a posterior distribution on
which we will denote by
. Since the parameter of interest
is a function of
, the posterior
for
defines a posterior distribution for
.
Now comes the interesting part. The likelihood has essentially no information in it.
To see that the likelihood has no information, consider a simpler case where is a function on
. Now discretize the interval into many small bins. Let
be the number of bins. We can then replace the function
with a high-dimensional vector
. With
, most bins are empty. The data contain no information for most of the
‘s. (You might wonder about the effect of putting a smoothness assumption on
. We’ll discuss this in Section 4.)
We should point out that if for all
, then Ericson (1969) showed that a certain exchangeable prior gives a posterior that, like the Horwitz-Thompson estimator, converges at rate
. However we are interested in the case where
is a complex function of
; then the posterior will fail to concentrate around the true value of
. On the other hand, a flexible nonparametric prior will have a posterior essentially equal to the prior and, thus, not concentrate around
, whenever the prior
does not depend on the the known function
. Indeed, we have the following theorem from Robins and Ritov (1997):
Theorem. (Robins and Ritov 1997). Any estimator that is not a function of cannot be uniformly consistent.
This means that, at no finite sample size, will an estimator that is not a function of
be close to
for all distributions in
. In fact, the theorem holds for a neighborhood around every pair
. Uniformity is important because it links asymptotic behavior to finite sample behavior. But when
is known and is used in the estimator (as in the Horwitz-Thompson estimator and its improved versions) we can have uniform consistency.
Note that a Bayesian will ignore since the
are just constants in the likelihood. There is an exception: the Bayesian can make the posterior be a function of
by choosing a prior
that makes
depend on
. But this seems very forced. Indeed, Robins and Ritov showed that, under certain conditions, any true subjective Bayesian prior
must be independent of
. Specifically, they showed that once a subjective Bayesian queries the randomizer (who selected
) about the randomizer’s reasoned opinions concerning
(but not
) the Bayesian will have independent priors. We note that a Bayesian can have independent priors even when he believes with probabilty 1 that
and
are positively correlated as functions of
i.e.
Having independent priors only means that learning
will not change one’s beliefs about
. So far, so good. As far as we know, Chris agrees with everything up to this point.
4. Some Bayesian Responses
Chris goes on to raise alternative Bayesian approaches.
The first is to define
Note that . Now we ignore (throw away) the original data. Chris shows that we can then construct a model for
which results in a posterior for
that mimics the Horwitz-Thompson estimator. We’ll comment on this below, but note two strange things. First, it is odd for a Bayesian to throw away data. Second, the new data are a function of
which forces the posterior to be a function of
. But as we noted earlier, when
and
are a priori independent, the
do not appear in the posterior since they are known constants that drop out of the likelihood.
A second approach (not mentioned explicitly by Chris) which is related to the above idea, is to construct a prior that depends on the known function
. It can be shown that if the prior is chosen just right then again the posterior for
mimics the (improved) Horwitz-Thompson estimator.
Lastly, Chris notes that the posterior contains no information because we have not enforced any smoothness on . Without smoothness, knowing
does not tell you anything about
(assuming the prior
does not depend on
).
This is true and better inferences would obtain if we used a prior that enforced smoothness. But this argument falls apart when is large. (In fairness to Chris, he was referring to the version from Wasserman (2004) which did not invoke high dimensions.) When
is large, forcing
to be smooth does not help unless you make it very, very, very smooth. The larger
is, the more smoothness you need to get borrowing of information across different values of
. But this introduces a huge bias which precludes uniform consistency.
5. Response to the Response
We have seen that response 3 (add smoothness conditions in the prior) doesn’t work. What about response 1 and response 2? We agree that these work, in the sense that the Bayes answer has good frequentist behavior by mimicking the (improved) Horwitz-Thompson estimator.
But this is a Pyrrhic victory. If we manipulate the data to get a posterior that mimics the frequentist answer, is this really a success for Bayesian inference? Is it really Bayesian inference at all? Similarly, if we choose a carefully constructed prior just to mimic a frequentist answer, is it really Bayesian inference?
We call Bayesian inference which is carefully manipulated to force an answer with good frequentist behavior, frequentist pursuit. There is nothing wrong with it, but why bother?
If you want good frequentist properties just use the frequentist estimator. If you want to be a Bayesian, be a Bayesian but accept the fact that, in this example, your posterior will fail to concentrate around the true value.
6. Summary
In summary, we agree with Chris’ analysis. But his fix is just frequentist pursuit; it is Bayesian analysis with unnatural manipulations aimed only at forcing the Bayesian answer to be the frequentist answer. This seems to us to be an admission that Bayes fails in this example.
7. References
Basu, D. (1969). Role of the Sufficiency and Likelihood Principles in Sample Survey Theory. Sankya, 31, 441-454.
Brown, L.D. (1990). An ancillarity paradox which appears in multiple linear regression. The Annals of Statistics, 18, 471-493.
Ericson, W.A. (1969). Subjective Bayesian models in sampling finite populations. Journal of the Royal Statistical Society. Series B, 195-233.
Foster, D.P. and George, E.I. (1996). A simple ancillarity paradox. Scandinavian journal of statistics, 233-242.
Godambe, V. P., and Thompson, M. E. (1976), Philosophy of Survey-Sampling Practice. In Foundations of Probability Theory, Statistical Inference and Statistical Theories of Science, eds. W.L.Harper and A.Hooker, Dordrecht: Reidel.
Robins, J.M. and Ritov, Y. (1997). Toward a Curse of Dimensionality Appropriate (CODA) Asymptotic Theory for Semi-parametric Models. Statistics in Medicine, 16, 285–319.
Robins, J. and Wasserman, L. (2000). Conditioning, likelihood, and coherence: a review of some foundational concepts. Journal of the American Statistical Association, 95, 1340-1346.
Rotnitzky, A., Lei, Q., Sued, M. and Robins, J.M. (2012). Improved double-robust estimation in missing data and causal inference models. Biometrika, 99, 439-456.
Scharfstein, D.O., Rotnitzky, A. and Robins, J.M. (1999). Adjusting for nonignorable drop-out using semiparametric nonresponse models. Journal of the American Statistical Association, 1096-1120.
Sims, Christopher. On An Example of Larry Wasserman. Available at: http://www.princeton.edu/~sims/.
Wasserman, L. (2004). All of Statistics: a Concise Course in Statistical Inference. Springer Verlag.
25 Comments
Fascinating stuff. But calling it “Frequentist pursuit” seems a bit harsh; Sims is mimicking the frequentist analysis because he knows that’s one that provides uniform consistency, thus enabling him to prove that *some* Bayesian approaches give reasonable estimators. (Clearly, some others don’t; it’s evidently possible to have bad priors that, despite the coherence of what they provide, don’t actually end up concentrating at the truth.) To prove that “Bayes fails”, as you suggest is admitted here, one would have to characterize the set of priors that don’t provide uniform consistency, and show that the prior one actually used had to lie in that set.
The only priors that can give uniform consistency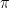 . There is no reason
. There is no reason
have to depend on
to choose such a prior except to mimic the frequentist answer.
–LW
Sims “round 2” states otherwise.
I’m surprised that Wasserman and Robins still don’t write down a correct likelihood, and don’t seem to acknowledge my assertion in the previous comment that they are not using a correct likelihood. My proposal did not rest mainly on smoothness for theta(). It rested mainly on recognizing that to write down the correct likelihood, a joint pdf for the observed random variables R, Y and pi, one has to take a position on the dependence between pi and theta, which requires introducing a new, infinite-dimensional parameter. And what I did involved no “frequentist pursuit” whatsoever. It is just straightforward infinite-dimensional Bayesian inference with the correct likellihood. The simple information-wasting Bayesian method I derived aimed at achieving simplicity by ignoring information, not at duplicating frequentist properties — it actually improves on Horwitz-Thompson without having started out with that objective.
I’ve written up a response, which is available, along with the original paper and some related slides, at sims.princeton.edu/yftp/WassermanExmpl. It’s the file with “R2”, for “round 2” at the end. Much of it repeats the discussion in the earlier paper, but since the example is slightly changed, and since this stuff seems to be challenging to understand, it may have beeen worthwhile rephrasing it.
Chris
Thanks for the comments.
We will reply in detail in a few days.
But two quick points:
1. Perhaps we weren’t clear about this but the are observed.
are observed.
2. Also, the marginal distribution for X is known (it is uniform).
Your response seems to treat the as unobserved.
as unobserved.
More later
–LW
@James and Larry:
Interesting. You start by stating a problem which is clearly horrendously underspecified – a priori, we can say that anyone claiming to provide an informative estimate for arbitrary choices of pi is wrong. For instance, whenever pi(x) is small for a large proportion of x values there is effectively no information available on which to base any inference. This is similar to the problem we face in science in general: given a system we know nothing about and a limited amount of data, predict something. Proceeding by constructing models/hypotheses and investigating whether they are supported by data is generally considered a good idea; proceeding by constructing model-free predictors for quantities of interest in a context of huge uncertainty regarding the processes that generate them is (in many contexts) considered unreliable.
You then present the Horwitz-Thompson estimator, but admit that it can be very inefficient (I imagine it is completely unuseable for the specific case (n=1000) of interest). You claim that this is remedied by an improved version, but give no way of evaluating its efficiency – how does it compare with the simple version and with the Bayesian solution? Why/how do you claim that the Bayesian solution fails to concentrate around the true value without making this comparison?
You point out that the likelihood function contains very little information – this is as it should be and provides a sanity check for likelihood-based approaches – since there is almost no information available about theta, any approach that claims to have access to such information should be distrusted. This would be a problem for a maximum likelihood approach that optimizes theta as an intermediate step (and due to numerical issues may be problematic for Bayesian methods in practice), but is not a problem for Bayesian approaches in theory – the marginalization step averages over the uncertainty in theta and may still get informative estimates for psi (when and only when that information is present in the data). Whether or not the likelihood function is informative for inference regarding theta is irrelevant to whether it is informative for inference regarding psi.
That said, your argument for the non-informativeness of the likelihood function is based on the absence of smoothness constraints. You then claim that introducing smoothness constraints when the problem is high dimensional will not help unless you make the function “very, very, very smooth”- but you do not quantify this. The thing to be quantified is not how much we know about theta (which remains very little), but how much we know about psi (after theta has been marginalised out). On what do you base the claim that “we have seen that response 3 doesn’t work” when you have made no attempt to quantify how well it actually does work or how it compares to your proposed solution?
Re priors: given the structure of the problem, and if interesting prior information about theta were available to be incorporated into the model, it is very feasible that such information would be highly dependent on pi — if we imagine this is an experimental setup which has been run before and from which we have drawn previous qualitative conclusions, those conclusions will have been much more informative when pi(x) was mostly large than when it was mostly small, and it would make sense to use a prior that is correspondingly tighter for larger pi. But I agree that one wants results that make sense even when the prior is independent of pi (from an objective Bayesian point of view, the prior is just another part of the model specification, which ought to be specified by the person posing the problem; also when we really know nothing about the system there doesn’t seem to be any reason to use a prior that depends on pi).
Finally, it is not clear how desirable uniform consistency (or any one specific frequentist metric) is, if (for instance) it is obtained at the expense of efficiency. Is a uniformly consistent estimator necessarily better than a pointwise consistent estimator? (In my limited understanding the main advantage of having uniform consistency is that it allows one to establish worst case guarantees on confidence interval size for finite sample sizes – this is not irrelevant, but one might be more interested in optimizing expected rather than worst case error.)
@Chris: What if we expand the problem statement as _specifying_ that pi and theta are independent (in the sense that knowing pi does not affect our knowledge of theta)? This seems reasonable when we have no relevant prior knowledge.
Good questions.
We’ll respond more fully i a few days.
The proof that the posterior does not concentrate is in the
Robins-Ritov paper.
–LW
@Konrad: As I point out in the “round 2” paper I linked to, the whole reason this problem is non-trivial is that pi and theta may be dependent. That is, it could be that the theta’s for the observations that are highly likely to have Y unobserved are quite different from the thetas of the observations where Y is likely to be observed . If theta and pi were independent, we could just throw out the observations where we don’t see Y and use the remaining sample as if there were no “R” variable. So specifying that theta and pi are independent is not a reasonable way to say we have little knowedge. It amounts to saying we are sure the main potential complication in the model is not present, and therefore opens us up to making seriously incorrect inference.
I think we are conflating different notions of independence. I have in mind a generative process that does have the sort of dependence you describe: P(Y|pi(x)) \neq P(Y), but where we have no prior information about the nature of this relationship, in the sense that our prior for theta when we do not know pi is unchanged when we learn pi: P(theta)=P(theta|pi). It seems to me that we can validly add that constraint to the problem specification without making it non-trivial.
You have to think through the full joint distribution implied by the conditions you are putting on pieces of it. P[Y=1 | pi(x)] is the same as E[ E [ Y | X] | pi(x)] = E[ theta(X) | pi(x)]. As the “round 2” paper shows, the distribution of the observables depends on the distribution of Y | pi(X) only through E[ theta(X) | pi(X)]. So if we follow your suggestion and insist that the distribution of theta does not depend on pi, there is no dependence between pi and theta remaining that can affect the distribution of the observables (or, therefore, be estimated).
Unfortunately I don’t have time to think about this properly now (hopefully I can get back to it soon). For now I just want to point out (echoing Entsophy below) that it’s very important to distinguish between (1) the probabilities involved in the generative process (what we might call “propensities”, or what Entsophy calls “frequencies” below – I’d argue that propensities and frequencies are still not conceptually identical, but that distinction is probably ok to ignore here) and (2) the (Bayesian) probabilities describing knowledge states. It’s also very important to be clear about when we are and when we are not conditioning on x – because y and r are dependent when we don’t condition on x and independent when we do. (@Jamie and Larry: x is observed in the stated setup, which means that our final inference relating to psi should be conditioned on x, but this doesn’t stop us from calculating the probabilities of various other quantities, some of which will _not_ be conditioned on x.) Above we are not very explicit about these issues, and this makes the discussion confusing (to me at least). At any rate, it’s not clear to me that the possible (but a priori unknown) dependency between the propensities pi(x) and theta(x) implies that the _prior_ distribution for theta(x) should be dependent on pi(x).
Larry,
If you begin a problem by estimating a “probability” then you’ll eventually run afoul of those who see “probabilities” as something different from “frequencies”. Probabilities P are something we Bayesians calculate given a state of knowledge. Frequencies F are relative ratios in the real world. They are different conceptually even when it happens that “P \approx F”.
Thinking hard about what frequencies one is trying to estimate here goes a long way to clearing the fog for a Bayesian. I suspect however that many simply don’t get the distinction and pointing this out will do nothing for them.
So moving on to something more constructive. The key here is to focus on the joint distribution p(x,y,r). Note that we actually know three things about the joint distribution p(x,y,r).
(1) We know the value of pi(x)
(2) We know the value of p(x)
(3) We know Y and R are independent given X.
conditions (1) and (2) can be expressed as linear constraints on the joint distribution p(x,y,r) (i.e. as averages of some function over the joint distribution). Condition (3) can be expressed as a non-linear constraint on the joint distribution.
This is important because theta(x) can be expressed as a linear constraint on the joint distribution as well (it’s something like the expected value of y times a delta function in x). So when you go to find a prior for theta, this prior has to be conditional on what we already know. In particular, the prior should be written:
p(theta | conditions (1), (2), (3))
Since the conditions (1), (2), (3) are all constraints on the joint distribution and theta can be calculated from the joint distribution, it is absolutely no surprise that this prior turns out to have a functional dependence on pi(x). Indeed this dependence is required for a Bayesian who consistently conditions their probabilities on what is assumed in the problem!
Also note: if all these conditions could be expressed as linear constraints on the joint distribution, then this point could be shown explicitly by using the maximum entropy principle to get a prior for theta that had a natural dependance on pi(x). Having said that however, if you just think harding at the beginning about what frequencie you’re actually want to predict, you can get a Bayesian answer with orders of magnitude less effort.
Very interesting (as Larry promised.)
If p(u,o) is an _acceptable_ joint distribution for unknowns and observed.
There must be a p(u) and p(u|o), o being observed (i.e. a region not a point).
Now p(u|o)/p(u) is the ratio of probabilities and is a multiple of the likelihood.
So it seem like there can’t be a problem or I am wrong about the above
(and some worthwhile stuff to learn for applications.)
Oops, I should have use un for unknown and kn for known: p(un,kn) instead of p(u,o) as observations are just one type of known. (And I’ll admit to finding suport for this in Chris’ round2 paper before “stepping into it again”.)
Jamie asked me to post this comment (LW)
Response To Sims’ Round 2: Part 1
by Jamie Robins
As did Chris let me state my main points before going into details.
1. I have no confusion about the example, not even lingering.
2. I have discussed the example with many individuals since it was published in 1997. Their counterarguments fall into 3 categories: (1) those that are incorrect, (2) those that are irrelevant to the example, (3) those that follow from misinterpreting or misreading. Every counterargument made by Chris in his “round 2 document ” has been made to me multiple times. None are novel.
3. In my experience the hardest part in discussing this example is overcoming the tendency of many to mush together separate issues. Therefore I will break the problem into logically separate pieces. In this way if there remains any disagreement between Chris and myself, all will know exactly where the disagreeement is.
Today I only take up the logically separate piece that necessarily
comes first: whether there are misreadings and/or misinterpretations
by Chris, as it is always possible that Chris disagrees with Larry and
I only because we were considering different problems. In fact such do
exist. So before going further I shall clear up these
misunderstandings and see if Chris still has any argument with our
post.
A ground rule for the discussion: In his Round 2 document, in at least 3 places, Chris returns to Larry’s 2004 example. That example, which I had nothing to do with, differs from this example . I’ll let Larry respond to Chris’s critique of that example if he wishes. But I ask Chris and others to henceforth restrict attention to the example in the blogpost (or to the original Robins-Ritov example from which it sprang if you like).
Chris’s Misreadings and Misinterpretations:
1 : Misreading and/or Misinterpretation re whether is observed
is observed
It is apparent from the last sentence of the first paragraph on his page 3 that Chris misreads the example and incorrectly assumes is not observed. Instead, Chris seems to believe that only the one dimensional function (coarsening)
is not observed. Instead, Chris seems to believe that only the one dimensional function (coarsening) 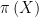 of
of  is observed where
is observed where 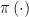 is the known propensity function.
is the known propensity function.
However the likelihood function given on the LHS of the first display is observed. Thus Chris seems to be analyzing a
is observed. Thus Chris seems to be analyzing a is observed is
is observed is
in section 3 of the blogpost clearly indicates that
different problem. The fact that
fairly central to our example as it is hard for a Bayesian to
justify throwing away so much information.
To summarize: The full data are iid
iid Here
Here  are
are is d-dimensional and continuous with
is d-dimensional and continuous with![{\left[ 0,1\right] ^{d}}](https://s0.wp.com/latex.php?latex=%7B%5Cleft%5B+0%2C1%5Cright%5D+%5E%7Bd%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) in
in
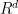 with d=100,000.
with d=100,000.
copies of
Bernouilli,
support on the unit cube
The observed data: are always observed and
are always observed and  is observed if and only if
is observed if and only if 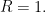 .
.
Equivalently, we observe iid copies of
iid copies of
Chris incorrectly says the observables are
Conclusion: Since is 100,000 dimensional and
is 100,000 dimensional and 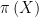 is 1 dimensional, Chris has assumed there is much less data available than there in fact is. Note that Chris’s remark that “
is 1 dimensional, Chris has assumed there is much less data available than there in fact is. Note that Chris’s remark that “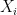 taking values in a high dimensional space is a redherring” would be correct were
taking values in a high dimensional space is a redherring” would be correct were  the observed data. However the observed data are
the observed data. However the observed data are  as a consequence
as a consequence  being high dimensional is anything but a red herring.
being high dimensional is anything but a red herring.
2. Misreading and/or Misinterpretation re whether the marginal density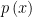 of
of  is known. We say the marginal density of
is known. We say the marginal density of  is uniform on
is uniform on ![{\left[ 0,1\right] ^{d}}](https://s0.wp.com/latex.php?latex=%7B%5Cleft%5B+0%2C1%5Cright%5D+%5E%7Bd%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) i.e.,
i.e., 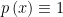 . We meant by that it was also known, but were not explicit.
. We meant by that it was also known, but were not explicit.
However the fact that we left out of the RHS of the first display in Sec 3 confirms that we are treating
out of the RHS of the first display in Sec 3 confirms that we are treating 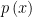 as known. The second display in Section 3 also indicates that
as known. The second display in Section 3 also indicates that 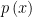 is known However Chris incorrectly states that the marginal density of
is known However Chris incorrectly states that the marginal density of  is unknown in his footnote on page 3.
is unknown in his footnote on page 3.
To summarize: In our example it is known that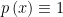
3: Why Chris may have made his misreadings:
Look at the RHS of the likelihood in the first display in section 3 of our blog post. Note even though data on is available, nonetheless , because
is available, nonetheless , because  the likelihood depends on
the likelihood depends on  only through
only through  and
and  This might make one erroneously believe that the actual observed data
This might make one erroneously believe that the actual observed data  could be reduced to
could be reduced to  by sufficiency. But this is incorrect because
by sufficiency. But this is incorrect because  is not sufficient for
is not sufficient for  If it were
If it were  would not depend on
would not depend on 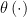 , but it does.
, but it does.
Note had we realized such misunderstandings might occur, we could and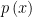 to be any
to be any but the constant 1 and then the
but the constant 1 and then the through
through
 and
and  In fact it is irrelevant to our
In fact it is irrelevant to our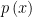 as known and uniform, known and not uniform, or
as known and uniform, known and not uniform, or
would have chosen
function of
likelihood would not only depend on
conclusions whether we regard \thinspace
unknown. We only chose known and uniform to simplify. In retrospect
this choice probably made the problem harder rather than easier to
understand.
Chris, with these clarifications, what disagreements remain?
Treating X as observed makes the likelihood you proposed correct, but leaves my main points unaffected. In order to undertake inference, we have to consider what might be reasonable beliefs about the joint distribution of the two random variables theta and pi. If we were certain that these random variables were independent, the model would be trivial, so no prior on theta() that explcitly or implicitly asserts that makes sense. So I guess our remaining disagreement is over the claim that a prior on the theta function that depends on the pi function can only arise from attempting to “mimic” frequentist procedures. I’ll expand on this this evening when I can use LaTeX.
Chris,
I haven’t read your comments in detail, but I think I came to some of the same conclusions from a different angle in the comments above. My basic point is that the following:
(a) Theta can be viewed as an expectation value over the joint distribution p(x,y,r)
(b) p(x,y,r) can’t be arbitrary because the prior information given in the problem consists of at least (3) constraint equations that p(x,y,r) has to satisfy.
(c) One of the constraints is given by the knowledge of pi(x), since pi() can be written as a funtional of p(x,y,r).
=> the prior for theta given the constraints on p(x,y,r) will have a natural dependce on pi(x)
Chris and
and  can be dependent (since they are both functions of X)
can be dependent (since they are both functions of X)
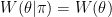 ?
?
Do you agree that the random variables
while the prior can make them independent functions i.e.
Larry
Well I don’t deny it, but I’ll try my point again from a more concrete angle:
Given the conditions in the problem you can write the joint in the following functional way:
p(x,y,r)=F(y, r, theta(x), pi(x))
for some function F. Given this relationship for a known pi(x) what is a reasonable prior for theta(x)?
We’ll here’s on natural criterion: theta_1 will have a higher prior probability than theta_2 if the entropy of the resulting p(x,y,r) is higher for theta_1 than it is for theta_2.
This natural criterion together with the functional relation F will make the prior for theta depend on pi! I’ll also note that it is easy to calulate F() and the resulting entropy of p(x,y,r) in terms of y,r,theta, and pi. So you can see the dependancy explicitly.
I take it back. The dependance on pi drops out. Ok, I’m convinced any natural prior for theta wont depend on pi.
Looking bleak, but just for the benefit of any students that might not know 😉
Rather than conditioning on ((p(x),pi(x)), O(X,R,YR)) {p,px being known functions}
what prevents one from conditioning instead on ((p(x),pi(x),MN(Y.i,p.IS(y)),O(X,R)) ?
{MN(Y.i,p.IS(y)) being the “known” importance sampling distribution of Y.i given pi(x.i) is known}
That is, trying to match the use of the importance sampling distribution by the Horwitz-Thompson estimator
by conditioning on that (perhaps stretching the meaning of known.)
I’ve written up a “round 3” comment, outlining a Bayesian approach to the problem with X observed. As you’ll see, it’s a lot like what I proposed in round 2, though I also suggest informally how to exploit smoothness if one thinks that likely. The main point again is that the prior on theta, which is a stochastic process with X as index, must have an unknown mean parameter, so that the prior does not implicitly assert precise knowledge of the parameter of interest, psi, before looking at the data.
I should have pointe out that round 3 is, like round 2, in the http://sims.princeton.edu/yftp/WassermanExmpl directory.
@normaldeivate: Larry: The fact that $\theta$ and $\pi$ both depend on $X$ does not mean that, before we observe any data, they are dependent. After all, all the random variables in the problem are functions of the state in an underlying probability space. Here $X$ might have two components, $X_1$ and $X_2$, that are independent, with $\pi$ a function of $X_1$ alone and $\theta$ a function of $X_2$ alone. And in this case the distribution of $\theta \mid \pi$ would not depend on $\pi$. So it is certainly possible to have a prior that makes $W(\theta\mid\pi)=W(\theta)$. It’s just that here that amounts to assuming at the outset that selection bias is not a problem, while the whole point of the example is that it \emph{is} a problem.
Dear Readers:
Since our reply is rather long, we are posting it as a new blog post. Please see:
–LW
2 Trackbacks
[…] Normal Deviate Thoughts on Statistics and Machine Learning Skip to content About « Robins and Wasserman Respond to a Nobel Prize Winner […]
[…] There are many other example such as this one. […]