SIMPSON’S PARADOX EXPLAINED

SIMPSON’S PARADOX EXPLAINED

Imagine a treatment with the following properties:

The treatment is good for men	(E1)
The treatment is good for women	(E2)
The treatment bad overall	(E3)

That’s the essence of Simpson’s paradox. But there is no such treatment. Statements (E1), (E2) and (E3) cannot all be true simultaneously.

Simpson’s paradox occurs when people equate three probabilistic statements (P1), (P2), (P3) described below, with the statements (E1), (E2), (E3) above. It turns out that (P1), (P2), (P3) can all be true. But, to repeat: (E1), (E2), (E3) cannot all be true.

The paradox is NOT that (P1), (P2), (P3) are all true. The paradox only occurs if you mistakenly equate (P1-P3) with (E1-E3).

1. Details

Throughout this post I’ll assume we have essentially an infinite sample size. The confusion about Simpson’s paradox is about population quantities so we needn’t focus on sampling error.

Assume that ${Y}$ is binary. The key probability statements are:

${P(Y=1\|X=1,Z=1) - P(Y=1\|X=0,Z=1) > 0}$	(P1)
${P(Y=1\|X=1,Z=0) - P(Y=1\|X=0,Z=0) > 0}$	(P2)
${P(Y=1\|X=1) - P(Y=1\|X=0) < 0}$	(P3)

Here, ${Y}$ is the outcome ( ${Y=1}$ means success, ${Y=0}$ means failure), ${X}$ is treatment ( ${X=1}$ means treated, ${X=0}$ means not-treated) and ${Z}$ is sex ( ${Z=1}$ means male, ${Z=0}$ means female).

It is easy to construct numerical examples where (P1), (P2) and (P3) are all true. The confusion arises if we equate the three probability statements (P1-P3) with the English sentences (E1-E3).

To summarize: it is possible for (P1), (P2), (P3) to all be true. It is NOT possible for (E1), (E2), (E3) to all be true. The error is in equating (P1-P3) with (E1-E3).

To capture the English statements above, we need causal language, either counterfactuals or causal directed graphs. Either will do. I’ll use counterfactuals. (For an equivalent explanation using causal graphs, see Pearl 2000). Thus, we introduce ${(Y_1,Y_0)}$ where ${Y_1}$ is your outcome if treated and ${Y_0}$ is your outcome if not treated. We observe

$\displaystyle Y = X Y_1 + (1-X) Y_0.$

In other words, if ${X=1}$ we observe ${Y_1}$ and if ${X=0}$ we observe ${Y_0}$ . We never observe both ${Y_1}$ and ${Y_0}$ on any person. The correct translation of (E1), (E2) and (E3) is:

${P(Y_1=1\|Z=1) - P(Y_0=1\|Z=1) >0}$	(C1)
${P(Y_1=1\|Z=0) - P(Y_0=1\|Z=0) >0}$	(C2)
${P(Y_1=1) - P(Y_0=1) <0}$	(C3)

These three statements cannot simultaneously be true. Indeed, if the first two statements hold then

$\displaystyle \begin{array}{rcl} P(Y_1=1) - P(Y_0=1) &=& \sum_{z=0}^1 [P(Y_1=1|Z=z) - P(Y_0=1|Z=z)] P(z)\\ & > & 0. \end{array}$

Thus, (C1)+(C2) implies (not C3). If the treatment is good for mean and good for women then of course it is good overall.

To summarize, in general we have

$\displaystyle (E1) = (C1) \neq (P1)$

$\displaystyle (E2) = (C2) \neq (P2)$

$\displaystyle (E3) = (C3) \neq (P3)$

and, moreover (E3) cannot hold if both (E1) and (E2) hold.

The key is that, in general,

$\displaystyle \begin{array}{rcl} P(Y=1|X=1,Z=1) &-& P(Y=1|X=0,Z=1)\\ & \neq & P(Y_1=1|Z=1) - P(Y_0=1|Z=1) \end{array}$

$\displaystyle \begin{array}{rcl} P(Y=1|X=1,Z=0) &-& P(Y=1|X=0,Z=0)\\ & \neq & P(Y_1=1|Z=0) - P(Y_0=1|Z=0) \end{array}$

and

$\displaystyle P(Y=1|X=1) - P(Y=1|X=0) \neq P(Y_1=1) - P(Y_0=1).$

In other words, correlation (left hand side) is not equal to causation (right hand side).

Now, if treatment is randomly assigned, then ${X}$ is independent of ${(Y_0,Y_1)}$ and

$\displaystyle P(Y=1|X=1,Z=z) = P(Y_1=1|X=1,Z=z) = P(Y_1=1|Z=z)$

and so we will not observe the reversal, even for the correlation statements. That is, when ${X}$ is randomly assigned, (P1-P3) cannot all hold.

In the non-randomized case, we can only recover the causal effect by conditioning on all possible confounding variables ${W}$ . (Recall a confounding variable is a variable that affects both ${X}$ and ${Y}$ .) This is because ${X}$ is independent of ${(Y_0,Y_1)}$ conditional on ${W}$ (that’s what it means to control for confounders) and we have

$\displaystyle \begin{array}{rcl} P(Y_1=1) &=& \sum_w P(Y_1=1|W=w) P(W=w)\\ &=& \sum_w P(Y_1=1|X=1,W=w) P(W=w) \\ &=& \sum_w P(Y=1|X=1,W=w) P(W=w) \\ \end{array}$

and similarly, ${P(Y_0=1) = \sum_w P(Y=1|X=0,W=w) P(W=w)}$ and so

$\displaystyle \begin{array}{rcl} P(Y_1=1) &-& P(Y_0=1)\\ & = & \sum_w [P(Y=1|X=1,W=w) - P(Y=1|X=0,W=w) ] P(W=w) \end{array}$

which reduces the causal effect into a formula involving only observables. This is usually called the adjusted treatment effect. Now, if it should happen that there is only one confounding variable and it happens to be our variable ${Z}$ then

$\displaystyle \begin{array}{rcl} P(Y_1=1) &-& P(Y_0=1)\\ &=& \sum_w [P(Y=1|X=1,Z=z) - P(Y=1|X=0,Z=z) ] P(Z=z). \end{array}$

In this case we get the correct causal conclusion by conditioning on ${Z}$ . That’s why people usually call the conditional answer correct and the unconditional statement misleading. But this is only true if ${Z}$ is a confounding variable and, in fact, is the only confounding variable.

2. What’s the Right Answer?

Some texts make it seem as if the conditional answers (P2) and (P3) are correct and (P1) is wrong. This is not necessarily true. There are several possibilities:

${Z}$ is a confounder and is the only confounder. Then (P3) is misleading and (P1) and (P2) are correct causal statements.
There is no confounder. Moreover, conditioning on ${Z}$ causes confounding. Yes, contrary to popular belief, conditioning on a non-confounder can sometimes cause confounding. (I discuss this more below.) In this case, (P3) is correct and (P1) and (P2) are misleading.
${Z}$ is a confounder but there are other unobserved confounders. In this case, none of (P1), (P2) or (P3) are causally meaningful.

Without causal language— counterfactuals or causal graphs— it is impossible to describe Simpson’s paradox correctly. For example, Lindley and Novick (1981) tried to explain Simpson’s paradox using exchangeability. It doesn’t work. This is not meant to impugn Lindley or Novick— known for their important and influential work— but just to point out that you need the right language to correctly resolve a paradox. In this case, you need the language of causation.

3. Conditioning on Nonconfounders

I mentioned that conditioning on a non-confounder can actually create confounding. Pearl calls this ${M}$ -bias. (For those familar with causal graphs, this is bascially the fact that conditioning on a collider creates dependence.)

To elaborate, suppose I want to estimate the causal effect

$\displaystyle \theta = P(Y_1=1) - P(Y_1=0).$

If ${Z}$ is a confounder (and is the only confounder) then we have the identity

$\displaystyle \theta = \sum_z [P(Y=1|X=1,Z=z)-P(Y=1|X=0,Z=z)] P(Z=z)$

that is, the causal effect is equal to the adjusted treatment effect. Let us write

$\displaystyle \theta = g[ p(y|x,z),p(z)]$

to indicate that the formula for ${\theta}$ is a function of the distributions ${p(y|x,z)}$ and ${p(z)}$ .

But, if ${Z}$ is not a confounder, does the equality still hold? To simplify the discussion assume that there are no other confounders. Either ${Z}$ is a confounder or there are no confounders. What is the correct identity for ${\theta}$ ? Is it

$\displaystyle \theta = P(Y=1|X=1) - P(Y=1|X=0)$

$\displaystyle \theta = \sum_z [P(Y=1|X=1,Z=z)-P(Y=1|X=0,Z=z)] P(Z=z)?$

The answer (under these assumptions) is this: if ${Z}$ is not a confounder then the first identity is correct and if ${Z}$ is a confounder then the second identity is correct. In the first case ${\theta = g[p(y|x)]}$ .

Now, when there are no confounders, the first identity is correct. But is the second actually incorrect or will it give the same answer as the first? The answer is: sometimes they gave the same answer but it is possible to construct situations where

$\displaystyle \theta \neq \sum_z [P(Y=1|X=1,Z=z)-P(Y=1|X=0,Z=z)] P(Z=z).$

(This is something that Judea Pearl has often pointed out.) In these cases, the correct formula for the causal effect is the first one and it does not involve conditioning on ${Z}$ . Put simply, conditioning on a non-confounder can (in certain situations) actually cause confounding.

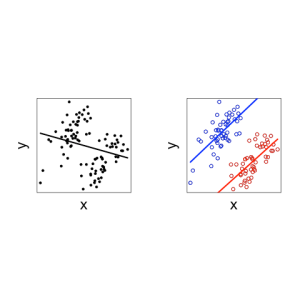
4. Continuous Version

A continuous version of Simpson’s paradox, sometimes called the ecological fallacy, looks like this:

Here we see that increasing doses of drug ${X}$ lead to poorer outcomes (left plot). But when we separate the data by sex ( ${Z}$ ) the drug shows better outcomes for higher doses for both males and females.

5. A Blog Argument Resolved?

We saw that in some cases ${\theta}$ is a function of ${p(y|x,z)}$ but in other cases it is only a function of ${p(y|x)}$ . This fact led to an interesting exchange between Andrew Gelman and Judea Pearl and, later, Pearl’s student Elias Bareinboim. See, for example, here and here and here.

As I recall (Warning! my memory could be wrong), Pearl and Bareinboim were arguing that in some cases, the correct formula for the causal effect was the first one above which does not involve conditioning on ${Z}$ . Andrew was arguing that conditioning was a good thing to do. This led to a heated exchange.

But I think they were talking past each other. When they said that one should not condition, they meant that the formula for the causal effect ${\theta}$ does not involve the conditional distribution ${p(y|x,z)}$ . Andrew was talking about conditioning as a tool in data analysis. They were each using the word conditioning but they were referring to two different things. At least, that’s how it appeared to me.

6. References

For numerical examples of Simpson’s paradox, see the Wikipedia article.

Lindley, Dennis V and Novick, Melvin R. (1981). The role of exchangeability in inference. The Annals of Statistics, 9, 45-58.

Pearl, J. (2000). Causality: models, reasoning and inference, {Cambridge Univ Press}.

13 Comments

Jared

Posted June 20, 2013 at 11:17 am | Permalink

It’s always surprised me that people find it astonishing that conditioning on a variable can induce confounding – in the very simplest case where there is no causal relationship between X and Y but they both have a causal effect on Z it seems obvious that conditioning on Z can render X and Y dependent. Striking examples are easy to come by too – suppose X,Y are independent Bernoulli and Z = X*Y (or X*Y+noise if the determinism is bothersome…).
- normaldeviate
  
  Posted June 20, 2013 at 11:24 am | Permalink
  
  Yes that example you give certainly makes it clear.
Norm Matloff

Posted June 20, 2013 at 12:29 pm | Permalink

In my open source book on probability and statistics heather.cs.ucdavis.edu/probstatbook I argue that it is only a “paradox” if one condiitons in the wrong order. If one conditions first on the most important predictor, and then adds the second predictor, the results are not at odds with each other.
- rj444
  
  Posted June 24, 2013 at 2:58 pm | Permalink
  
  what do you mean by “most important”? A forward selection type procedure does nothing to address simpson’s paradox (as Jared points out above, it can induce confounding), but maybe you have something else in mind.
kenmccue

Posted June 20, 2013 at 6:13 pm | Permalink

Any thoughts (or literature references) for determining what the “correct” confounding variable is (or, conversely, how do you know if you have the wrong one)?
- normaldeviate
  
  Posted June 21, 2013 at 3:27 am | Permalink
  
  That’s the million dollar question.
  Of course you can use variable selection methods.
  But you also have to depend on subject matter knowledge.
  And there is no escaping the fact that there will always be
  some unobserved confounders.
  - Norm Matloff
    
    Posted June 23, 2013 at 11:29 pm | Permalink
    
    Regarding ordering the variables, all I had in mind was taking action if Simpson’s Paradox is observed. It should be a clue that some other variable should be brought into the analysis first, i.e. the existing ordering should be changed. That should be easy.
kenmccue

Posted June 21, 2013 at 7:22 pm | Permalink

Incidentally, I disagree with your characterization of the ecological fallacy

A continuous version of Simpson’s paradox, sometimes called the ecological fallacy…

The ecological “fallacy” was noted by Goodman, who noted that when individual-level data was aggregated, the correlation between two variables was typically different than when individual-level data was available and the correlation was calculated using the individual-level data. His solution was to use linear regression, which gave the same estimate as the individual level estimate of proportion. In a classic case, if the percent of one group supporting a candidate is calculated using the individual data (which is then just the mean of the vote for that candidate, if vote choice is coded 0-1) as it is for the regression estimate (essentially, in an election unit, let V be the vote for the candidate, X1 being the number in group one, p1 being the proportion voting for the candidate in group1, X2 being the number in group 2, p2 being the proportion voting for the candidate in group2, then V = X1p1 + X2p2 = X1p1 + X2p1 – X2p1 + X2p2 = (X1 + X2)p1 + X2(p2 – p1) which gives %Vote = a + %X2b, where b = p2 – p1, a = p1, and %V is percent vote for a candidate and %X2 is percent in group 2). Then the estimates for p1 and p2 from the regression will be approximately the same as from using the individual data _except_ for the empirical fact that the consistency of the p1 and p2, implicitly assumed in the regression, is rarely true. The relationship of the correlation coefficient and violations of this consistency assumption with its implications for regression analysis (including a theory of how central limiting processes imply a distribution on the error in the regression) are discussed at some length in

Arthur Lupia and Kenneth F. McCue. 1990. “Why the 1980’s Measures of Racially Polarized Voting Are Inadequate for the 1990’s.” Law and Policy 12: 353-387.

but it is the violation of the consistency of the coefficients between electoral units that gives the relation to SImpson’s paradox, so the ecological fallacy is a specialized subset of the paradox. In particular, in the example you give above about a drug interaction and gender, there is no aggregate data involved, and hence the term ecological fallacy, as is commonly used in the social science literature, would not be appropriate. It is appropriate to note that Simpson’s paradox (which I would interpret as multiple regimes generating the data) has made it very difficult to do ecological analysis.
- normaldeviate
  
  Posted June 22, 2013 at 2:32 am | Permalink
  
  ok thanks for the clarification
JRaSH

Posted June 23, 2013 at 11:02 am | Permalink

I guess in the beginning of section 2, instead of ‘Some texts make it seem as if the conditional answers (P2) and (P3) are correct and (P1) is wrong.’, what you’re trying to say is ‘Some texts … (P1) and (P2) are correct and (P3) is wrong.’
- normaldeviate
  
  Posted June 23, 2013 at 11:17 am | Permalink
  
  right thanks
Simon Goring

Posted June 29, 2013 at 1:09 pm | Permalink

There’s a nice article by Jim Clark et al. that talks about Simpson’s Paradox in Ecology Letters, with a good representation and explanation in Figure 1:
Clark JS, Bell DM, et al.. (2011). Individual‐scale variation, species‐scale differences: inference needed to understand diversity. Ecology Letters, 14(12), 1273-1287. http://dx.doi.rg/10.1111/j.1461-0248.2011.01685.x
Geo

Posted May 19, 2014 at 8:15 am | Permalink

This is often more of an issue when one does observational studies, as is often encountered in practical disciplines such as web traffic analysis for the purpose of internet marketing. I give some examples and explanations here: http://blog.analytics-toolkit.com/2014/segmenting-data-web-analytics-simpsons-paradox/