A few months ago I posted about John Ioannidis’ article called “Why Most Published Research Findings Are False.”
Ioannidis is once again making news by publishing a similar article aimed at neuroscientists. This paper is called “Power failure: why small sample size undermines the reliability of neuroscience.” The paper is written by Button, Ioannidis, Mokrysz, Nosek, Flint, Robinson and Munafo.
When I discussed the first article, I said that his points were correct but hardly surprising. I thought it was fairly obvious that 
The new paper has basically the same message although the emphasis is on the dangers of low power. Let us assume that for a fraction of studies 
Let us suppose, for the sake of illustration that 
So indeed, if the power is low, the chance of a false discovery is high. (And things are worse if we include the effects of bias.)
The authors go on to estimate the typical neuroscience studies. They conclude that the typical power is between .08 and .31. I applaud them for trying to come up with some estimate of the typical power but I doubt that the estimate is very reliable.
The paper concludes with a number of sensible recommendations such as: performing power calculations before doing a study, disclosing methods transparently and so on. I wish they had included one more recommendation: focus less on testing and more on estimation.
So, like the first paper, I am left with the feeling that this message, too, is correct, but not surprising. But I guess that these points are not so obvious to many users of statistics. In that case, papers like these serve an important function.
Normal Deviate 
19 Comments
A power of one gives you a probability of false discovery of 0.3 ???
Oh, low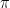
… all right.
With high power, although there will be false positives I would assume that the confidence interval would be close to the null, indicating that the difference was not of practical significance. Generally for underpowered experiments when significant the confidence interval will extend into regions which are not plausible, something that researchers should be made aware of as a check for a well conducted experiment.
Right. That’s why I prefer to emphasize estimation over testing.
By P(A|H_0), do you mean P(A; H_0)?
In this post I am thinking of a population of testing situations and I
am explicitly making H0 random
Thanks for the response.
I have a follow-up question: Can a one-off hypothesis test be construed as a sample from a population of testing situations? If so, does it then make sense to talk about P(A|Ho) in that setting? If not, why not?
I’m also curious about estimation vs. testing. Correct me if I’m wrong, but don’t (some of) the same basic testing issues come up in estimation, too? For example, if we estimate a model parameter (e.g., a coefficient in a linear model), if we want to infer something about that parameter (and whatever it’s expressing with respect to our data), don’t we (often) end up being concerned about, say, whether the parameter (plus/minus a suitable measure of error) is greater or less than zero? This seems to me to be a special case of hypothesis testing, and so beset by the same problems.
re your first question: you can talk about P(A|H0) in a one-off situation
if you are using a Bayesian approach but I have in mind here that pi is
a real frequency not a prior.
re second question: if we only care about whether 0 is in the interval
than yes it is the same as testing. By focusing more on estimation I meant,
putting less emphasis on the 0 versus nonzero question
This will be a quick remark (or at least a messy one) since I’m traveling. Mixing power in with this “frequentist Bayesian” computation is very misleading—even if it’s all relative frequencies. Power is to be computed relative to a discrepancy from a given null or test hypothesis of interest. Instead you or they are using it in the context of a pool or urn of nulls, from which, presumably, you are to randomly sample hypotheses. The fact that a particular null hypothesis Hi was randomly selected from a pool of nulls, 90% of which are assumed “true” (and never mind how you can know this), may allow you to assign
probability .9 to the event of selecting a true null, but this number has nothing to do with any kind of evidential assessment of the truth of Hi. Nor does the posterior. It confuses evidence for the occurrence of an event, given a fully specified (if questionable) probability context, with evidence for discrepancies from a given null actually evaluated.
(Ironically, it is commonplace to say “all nulls are false”, whereas you’ve got 90% true nulls.) I’m not saying this context cannot happen, I’m saying that it has nothing to do with the use of statistical tests in science in appraising a given hypothesis.
What pool of nulls to use? Are you prepared to allow that were null hypothesis Hi to have been selected from an urn with a small enough frequency of true nulls, so as to obtain a low posterior relative frequency, that this same exact statistically significant result is good evidence against the particular Hi chosen? This would confuse the scientific interest in evidence of discrepancies of various amounts from a given null, with an interest in rates of “true/false” outputs. Only in the most behavioristic settings could this be relevant. (Note, too, that wrt a given null hypothesis, the higher the power, the easier it is to reject with a trivial discrepancy.) I really hope that you clarify these points with the authors who are keen to produce such utterly non-surprising results. Anyway, the peril is not with significance tests, but with encouraging variations on a well-known howler against them:
+1
Larry pretty clearely was just estimating a frequency and didn’t make the errors you seem to be attributing to him. It’s nice though to see you drawing a clear distinction between the frequency with which something is true, and the evidence we have that something is true. It’s almost like they’re two distinct things.
The “and never mind how you can know this” comment was a nice touch too. Statistics seems to be rife with things which we are supposed to verify objectively but which statisticans give no hints as to how this should be done. So how exactly are we supposed to verify at the time an inference is made that future errors will follow a given pattern anyway?
I’m at a conference now
Will reply in more detail when I get back
Larry
“(Ironically, it is commonplace to say “all nulls are false”, whereas you’ve got 90% true nulls.)”
I think we’re mixing up different notions of null hypotheses in different contexts here. There’s the question of whether the random process described by the null distribution describes the data that one has. In observational settings, this is always false. Incidentally, usually when I hear the “all nulls are false”, it’s in the context of a domain where observational data are the norm. Then there’s the question of whether one’s hypothesis is correct or not. Most hypotheses turn out to be false. This is the context in which Ioannidis is proposing his 90% number (part of the confusion stems from the abuse of NHST with “the null hypothesis is false, therefore my theory is correct” logic).
Another way of looking at this is that nature’s causal graph is sparse but it is also connected. There’s no contradiction.
I was going to be picky about Larry’s comment (And things are worse if we include the effects of bias.) which is not quite right as bias can mask true effects resulting as a pseudo null that we actual want to be declared false, because it is.
So in observational settings it makes no sense to think in terms of power and type one error but most of our client applications are in observational settings.
No wonder there is such widespread confusion.
By the way, I believe WG Cochrane the first point out (roughly 1970’s) that with confidence intervals in an observational setting, small sample sizes result in better coverage with large enough samples providing near zero coverage!
Interesting results and thoughts. Here is a little comic relief on the ‘null hypothesis’. http://www.statisticsblog.com/2013/04/sudden-clarity-about-the-null-hypothesis/
Firstly, I would agree that results of significance tests should always be interpreted in terms of the discrepancies from a test hypothesis that have and have not been indicated severely (at least wherever possible). (So I am in sync with the call for CIs rather than “up-down” tests) But if a statistically significant result at a given level is found with a test despite having low power, that result indicates a greater discrepancy from the null than if it arose from one with a higher power. So they ought to look at the discrepancies indicated with their low powered tests, rather than dismiss them. I keep to power here, even though I prefer the data dependent scrutiny offered by SEV. (Power considers the worst case of just barely rejecting). But the reasoning is otherwise similar. That Larry indicates the example is open to a confidence interval estimation (rather than having to be a dichotomous ruling) shows the example is open to this type of an assessment. Whether they should increase the power of their tests should depend on the extent of discrepancy of interest, not the desire to decrease the type2 error rate over a pool of different nulls–I haven’t read their article, could only get the abstract. They may otherwise be picking up on trivial discrepancies–recall the whole “large n” problem. Second, I’m not saying the relative frequency assessment over a pool of nulls is incorrect, only that it is not what needs to be assessed in scrutinizing the evidential import of a statistically significant result from a given Ho–at least, as I see it. (I also don’t think the term used in the computation should be called power, but won’t argue about that.) See various discussions of fallacies of rejection.
http://errorstatistics.com/2012/10/21/mayo-section-6-statsci-and-philsci-part-2″/ (section 6.1.3–very short).
Confidence intervals also call for a post-data SEV assessment.
I think the point was not regarding evaluation of evidence, but to criticize the usual practice in some areas of neuroscience of using extremely small samples. The justification is, similar to what you state, that with small samples hits represent large deviations which may be more important / more likely to be true. It’s reasonable to then look at the frequency properties of such a strategy over eg all experiements in a field. The reliability of the small-n strategy given real world model mis-specification, experimental error, and bias are separate discussions. Of course, these small-n hits also tend to represent when the noise lines up with the signal and create replication problems.
ps: spell check recommends I replace “neuroscience” with “pseudoscience” 😛
we read you downunder.
Only just caught up with you so hopefully you wil lget some readers from down here.
keep it up
2 Trackbacks
[…] The Perils of Hypothesis Testing … Again […]
[…] Ok so (1) 90% of the hypotheses that scientists consider are false. Let be the power. Then the probability of a false discovery, assuming we reject Ho at the α level is given by the computation I’m pasting from an older article on Normal Deviate’s blog. […]